Edgeworth-Box

Indifferenzkurven für zwei Güter x und y.

Edgeworth-Box mit Tauschvorgang; der von den dicken Linien begrenzte Bereich wird auch Tauschlinse genannt.

Die Optimierung durch Tauschvorgänge definiert die Kontraktkurve.

Die Edgeworth-Box (nach Francis Ysidro Edgeworth) ist ein grafisches Konstrukt, das sich aus zwei Diagrammen mit Indifferenzkurven zusammensetzt.

Sie geht eigentlich auf Pareto zurück, wurde jedoch zu Ehren des Philosophen und Wirtschaftswissenschaftlers Edgeworth benannt, der die Methode als einer der ersten im großen Stil angewandt hat. Sie wurde zu einem gängigen Werkzeug der Allgemeinen Gleichgewichtstheorie und wird gelegentlich auch als Tauschbox bezeichnet. Die Edgeworth-Box eignet sich zur Analyse der Allokation von zwei verschiedenen Gütern zwischen zwei Individuen in einer (Tausch-)Wirtschaft in der Haushaltstheorie oder auch der Aufteilung zweier Inputfaktoren auf zwei Unternehmen in der Produktionstheorie.

Die Grafik zeigt die Indifferenzkurve für zwei Güter. So ist der Besitz von drei Einheiten auf der X-Achse und drei Einheiten auf der Y-Achse gleichwertig mit dem Besitz von einer X-Einheit und neun Y-Einheiten. Anschaulich drückt die Kurve die Präferenz aus, von beiden Gütern möglichst gleich viel zu besitzen. Als Beispiel wurde die Indifferenzfunktion $I(x,y)=\sqrt{x \cdot y}$ gewählt. Das entsprechende Konturdiagramm zeigt Hyperbeln für die Werte 3 bis 8.

Die Edgeworth-Box entsteht durch die Zusammenlegung von zwei binären Koordinatensystemen, welche jeweils ein Wirtschaftssubjekt repräsentieren (oder: ein Wirtschaftssubjekt und das Aggregat aller anderen Wirtschaftssubjekte). Die sich gegenüberliegenden Ursprünge stellen jeweils die Punkte dar, in denen das eine Individuum alle Einheiten der betrachteten Tauschgüter besitzt und das andere keine. Der durch die 2x2 Achsen aufgespannte Raum stellt grafisch die Menge aller theoretisch möglichen Verteilungen der beiden Güter dar, wobei die Achsenlänge jeweils die gesamte vorhandene Menge des abgebildeten Gutes darstellt.

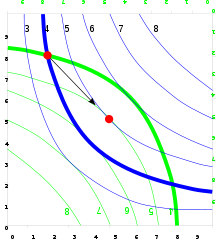
Bündel von Indifferenzkurven (Linien, die alle Güterkombinationen mit jeweils gleichem subjektivem Wert abbilden) innerhalb der Edgeworth-Box bilden die Präferenzen der Wirtschaftssubjekte ab. Dabei zeigen die Indifferenzkurven des Individuums A, dessen Koordinatenursprung links unten ist (blau), in Richtung rechts oben zunehmende Nutzen. Umgekehrt steigt der Nutzen von Individuum B (Ursprung rechts oben, grün) mit der Verschiebung der Indifferenzkurven nach links unten.

Wenn nun in der Grafik der obere Schnittpunkt die anfängliche Verteilung (Anfangs-Allokation) der Güter X und Y auf die Individuen Blau und Grün darstellt, gibt jene Indifferenzkurve, die diesen Punkt beinhaltet, das aktuelle Nutzenniveau an. In dieser Situation können beide Individuen durch Tausch einen höheren Nutzen erreichen. Im Bereich innerhalb der "Linse", die durch die beiden Indifferenzkurven dargestellt wird, erreichen beide Wirtschaftssubjekte ein höheres Nutzenniveau, ohne den jeweils anderen zu schädigen. Eine solche Situation ist strikt besser − oder pareto-superior − gegenüber der Ausgangssituation. Der freiwillige Tausch wird nun genau solange stattfinden, bis die Indifferenzkurven keine Linse mehr bilden, sondern sich nur noch in einem Punkt berühren (unterer roter Punkt). Diese Kontraktkurve ist die Gleichgewichtsallokation, weil hier der Tausch zum Erliegen kommt und ein Marktgleichgewicht hergestellt ist.

Die orangen Punkte sind weitere Möglichkeiten der Pareto-Optimierung. Jeder der Punkte erfüllt die Voraussetzung, dass sich kein Partner verbessern kann, ohne dass der andere schlechter gestellt wird. Bei Bewegungen auf der Kontraktkurve sind also keine Pareto-Verbesserungen mehr möglich. Im Beispiel ist die Kontraktkurve eine Gerade, da die Hyperbeln der Indifferenzfunktion $\sqrt{x \cdot y}$ spiegelsymmetrisch sind.

Siehe auch

• Wohlfahrtstheoreme