Indifferenzkurve

Indifferenzkurven zweier Güter mit vier, im Text besprochenen Punkten

Die Indifferenzkurve (lat. indifferens: „sich nicht unterscheidend“; auch Isonutzenkurve oder Isonutzenlinie) stellt alle Gütermengenkombinationen (die so genannten Güterbündel) dar, zwischen denen ein Haushalt gemäß seinen Präferenzen indifferent ist, die er also als gleich gut einschätzt. Die Güterbündel, die auf derselben Indifferenzkurve liegen, stiften dem Haushalt den gleichen Nutzen.

Der Ausdruck geht auf Francis Ysidro Edgeworth zurück und wurde von Vilfredo Pareto in die Wirtschaftstheorie eingeführt, um das (bis heute nicht befriedigend gelöste) Problem der Nutzenmessung zu umgehen. Auf ihr basiert die so genannte Edgeworth-Box.

Konstruktion

Zur Konstruktion der Indifferenzkurven wird auf der horizontalen Achse eines Koordinatensystems die Menge des Konsums an Gut 2 und auf der vertikalen Achse die Menge des Konsums an Gut 1 dargestellt. Unter der Annahme, dass beide Güter unendlich teilbar sind, kann man unendlich viele Punkte in das Koordinatensystem einzeichnen, zwischen denen das Individuum indifferent ist. Die sich somit ergebende Linie ist die gesuchte Indifferenzkurve.

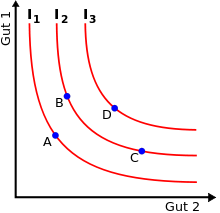
Im nebenstehenden Beispiel sind drei Indifferenzkurven eingezeichnet. Unter den vier eingezeichneten Punkten wird A am geringsten geschätzt, D am meisten. B und C liegen auf derselben Indifferenzkurve, d. h., dem Individuum ist es egal, ob es das Güterbündel B oder C konsumiert. Als anschauliches Beispiel kann man sich vorstellen, dass es sich bei Gut 1 um die Freizeit und bei Gut 2 um das Einkommen handelt, die dem Individuum jeweils zur Verfügung stehen.

Annahmen und Eigenschaften

Da per definitionem Indifferenzkurven die subjektiven Präferenzen eines Individuum widerspiegeln, sind die Eigenschaften der Indifferenzkurven durch dieses Individuum bestimmt. Stellt man aber gewisse (Grund-)Annahmen über das Verhalten von Individuen auf, so kann man daraus auf die generellen Eigenschaften von Indifferenzkurven schließen. Folgende Annahmen werden in der Regel getroffen:

• Nichtsättigung,
• Stetigkeit,
• Transitivität,
• Konvexität.

Nichtsättigungsannahme

Man geht jeweils davon aus, dass ein Individuum lieber mehr von einem Gut hat als weniger. Ein Güterbündel wie D in obiger Abbildung, das von beiden Gütern mehr enthält als das Güterbündel A, wird gegenüber Güterbündel A stets vorgezogen, beide können nicht auf derselben Indifferenzkurve liegen. Daraus ergibt sich unmittelbar, dass bei Gültigkeit dieser Annahme der Nichtsättigung Indifferenzkurven (wie in obiger Abbildung) eine negative Steigung ($-\infty$ und 0 eingeschlossen) haben müssen.

Stetigkeitsannahme

Dies ist eine sehr formale Annahme, die aber benötigt wird, um die Existenz von Indifferenzkurven sicherzustellen.

Geht man - wie in der Abbildung - von drei Alternativen A, B und D aus, bei der B dem A und D dem B vorgezogen wird, so soll es in der konvexen Kombination von A und D (also dem Geradenstück zwischen A und D) stets einen Punkt geben, der indifferent zu B ist.

Diese Annahme ist bei der lexikographischen Präferenzordnung nicht erfüllt. Bei dieser Präferenzordnung existieren somit keine Indifferenzkurven.

Transitivitätsannahme (oder Konsistenzannahme)

Aus obiger Grafik ist bereits eine wichtige Eigenschaft der Indifferenzkurven sichtbar: Indifferenzkurven können einander nicht schneiden (wie auch Höhenlinien an einem "echten" Berg einander nicht schneiden können). Dies entspricht dem Grundsatz, dass die Rangfolge der Güterbündel widerspruchsfrei sein muss (Transitivität). Wenn ein komplettes Nutzengebirge dargestellt werden soll, dann besteht dies aus einer unendlich großen Schar von Indifferenzkurven.

Beispiel für Transitivität: Wenn eine Person Äpfel mehr mag als Birnen und Birnen mehr mag als Bananen, dann ergibt sich aus dem Grundsatz der Transitivität zwingend, dass diese Person Äpfel auch Bananen vorzieht.

Konvexitätsannahme (oder Ausgewogenheitsannahme)

In allgemeinen Fällen werden üblicherweise konvexe Indifferenzkurven angenommen, diese garantieren einen negativen Substitutionseffekt. Besonders häufig wird dabei von Cobb-Douglas-Nutzenfunktionen ausgegangen.

Im Bild sind die Indifferenzkurven konvex. Die Form der Indifferenzkurven weist darauf hin, in welcher Form der Haushalt bereit ist, Gut 1 für Gut 2 zu substituieren. Der Betrag der Neigung der Kurve an den einzelnen Punkten gibt an, wie viele Einheiten von Gut 1 im Austausch für eine Einheit des Gutes 2 benötigt werden, um auf dem gleichen Niveau zu bleiben. Dies wird Grenzrate der Substitution genannt. Wenn man eine der Indifferenzkurven wie im Beispiel von oben nach unten durchläuft, so wird stets von Gut 1 mehr und von Gut 2 weniger konsumiert, ohne dass sich der erreichte Nutzen ändert: Gut 2 wird bei konstantem Nutzen durch Gut 1 substituiert. Dies ist das Gesetz von der abnehmenden Grenzrate der Substitution.

Wenn von einem Gut viel substitutiert wurde, ist es verhältnismäßig knapp. Darum werden viele Einheiten des anderen Gutes zur Substitution benötigt. Der daraus resultierende konvexe Kurvenverlauf zeigt, dass der Haushalt Güterbündel mit gemischtem Inhalt solchen vorzieht, die einseitig viel von Gut 1 oder Gut 2 beinhalten. In der Grafik lässt sich dies zeigen, wenn man eine Verbindungslinie zwischen den Punkten B und C ziehen würde. Jeder Punkt auf dieser Linie würde der Haushalt den Punkten B oder C vorziehen, da diese auf höheren Indifferenzkurven liegen. (Regel: „Durch Mischen stellt sich der Haushalt besser.“)

Unterschieden werden kann weiterhin zwischen starker bzw. strikter Konvexität (wie im obigen Beispiel), in diesem Fall werden ausgewogene Konsumbündel strikt bevorzugt, erreichen also immer ein höheres Nutzenniveau als weniger ausgewogene Güterbündel. Liegt lediglich Konvexität (wird auch als schwache Konvexität bezeichnet) vor, haben die entsprechenden Indifferenzkurven einen Abschnitt mit konstanter Steigung. Hier werden ausgewogene nicht mehr zwangsläufig bevorzugt. Im obigen Beispiel würde das bedeuten, dass die Punkte B und C sowie die Punkte auf der sie verbindenden Linie auf derselben Indifferenzkurve liegen, der Konsument ist dann indifferent.

Beweis

Beweis für die Konvexität von Indifferenzkurven:^[1]

Bedingung für Konvexität

$\frac{d^2x_1}{dx_2^2} \ge 0$

wobei

$\frac{dx_1}{dx_2} = -\frac{f_2(\varphi(x_2),x_2))}{f_1(\varphi(x_2),x_2))}$

und φ(x₂) = x₁

$\Rightarrow \frac{d^2x_1}{dx_2^2} = - \frac{[f_1 \cdot (f_{12} \cdot \varphi'(x_2)+ f_{22})-f_2 \cdot (f_{11} \cdot \varphi'(x_2)+ f_{12})]}{f_1^2} > 0\ |\cdot f_1^3$

dabei gilt

$f_{12} = f_{21} \!$ und $\varphi'(x_2) = -\frac{f_2}{f_1}$

$\Rightarrow 2 \cdot f_{12}f_1f_2 - (f_1^2f_{22}+f_2^2f_{11}) > 0$

gilt, da

$f_{12}>0,\ f_{22}<0,\ f_{11}<0$

Beispiele

Indifferenzkurven können auch linear sein. Dies bedeutet, dass der Haushalt bereit ist, Gut 1 und Gut 2 entlang der gesamten Kurve zu einem festen Verhältnis zu tauschen. Man spricht von "perfekten Substituten". Dies sind Güter, die problemlos gegeneinander ausgetauscht werden können - es dem Haushalt also egal ist, ob er mehr von Gut 1 oder mehr von Gut 2 konsumiert.

Perfekte Komplemente sind eine weitere Sonderform. Hier haben die Indifferenzkurven einen Knick (L-förmig). Dies bedeutet, dass der Konsument Gut 1 und Gut 2 in einem fixen Verhältnis konsumieren möchte. Gibt man ihm nur mehr von einem der beiden Güter, so erhöht dies seinen Nutzen nicht. Ein Beispiel hierfür sind linke und rechte Schuhe. Kauft man fünf linke und fünf rechte Schuhe, so bringt das Kaufen von 5 weiteren linken Schuhen keinen Mehrnutzen.

Ausnahmeformen von Indifferenzkurven

Die folgenden Formen entsprechen nicht den Standardannahmen:

Konkave Indifferenzkurven besagen, dass der Haushalt Güterbündel bevorzugt, die einseitig viel von einem der beiden Güter enthalten. (Regel: "Extreme werden bevorzugt.") Beispiele sind lokal gebundene Güter: Ein Haushalt, der ein Grundstück von 300 m² in Berlin und ein weiteres von 300 m² in München besitzt, wird in der Regel demgegenüber ein einziges von 600 m² in einer der beiden Städte präferieren.

Auch kreis- oder ellipsenförmige Indifferenzkurven sind denkbar. Hier existiert ein zentraler Punkt, der in der Mitte der runden Indifferenzkurven liegt. An diesem „Bliss-Punkt“ hat der Haushalt sein maximales Nutzenniveau erreicht. Ein Haushalt mit einer solchen Präferenzordnung wird dann nicht knappe Güter (die es im "Bliss-Punkt" nicht gibt), gegen andere knappe Güter einhandeln. Damit ist der Haushalt für eine Preistheorie irrelevant.

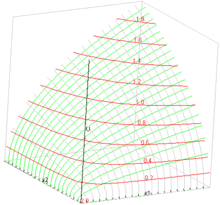Nutzengebirge einer Cobb-Douglas-Nutzenfunktion

Nutzengebirge

Jedem Punkt im Indifferenzkurvensystem kann ein Nutzenindex zugeordnet werden, der folgende Bedingungen erfüllt, sonst aber beliebig ist:

1. Zwei Punkte, zwischen denen das Individuum indifferent ist, die also auf derselben Indifferenzkurve liegen, erhalten den gleichen Nutzenindex.
2. Wird eine Kombination einer anderen vorgezogen, so erhält sie einen höheren Nutzenindex.

Dann kann man in ein dreidimensionales Koordinatensystem den Nutzenindex als dritte Dimension hinzufügen. Ermittelt man den Nutzenindex für alle möglichen Güterbündel aus Gut 1 und Gut 2, so erhält man einen Nutzenberg oder ein Nutzengebirge. Die Indifferenzkurve ergibt sich in einem Nutzengebirge als eine Höhenlinie. Sie kommt durch einen waagrechten Schnitt des Gebirges zustande. Man beachte, dass man je nach gewähltem Nutzenindex unterschiedliche Gebirge erhält, dass diese aber alle das gleiche Indifferenzkurvensystem besitzen.

Haushaltsoptimum

Steigung der Indifferenzkurve und Grenzrate der Substitution

Die Grenzrate der Substitution oder Steigung der Indifferenzkurve dx₂ / dx₁ bezeichnet das Austauschverhältnis zwischen den Gütern, bei dem sich das Versorgungsniveau aus Sicht des Haushaltes, also subjektiv, nicht ändert. Bei der optimalen Konsumentscheidung eines Haushaltes (dem Haushaltsoptimum) hat die Grenzrate der Substitution denselben Wert wie die Steigung der Budgetgeraden − p₁ / p₂ (anschaulich im nachfolgendem Beispiel). Das bedeutet, dass sich die Indifferenzkurve und die Budgetgerade in diesem Punkt berühren (nicht schneiden).

Grenzrate der Substitution (1. Ableitung der Indifferenzfunktion) = Preisverhältnis (1. Ableitung der Budgetgeraden)

Daraus ergibt sich die Gültigkeit des 2. Gossenschen Gesetzes.

Analogie

Die gleiche Sichtweise ist auch in der Produktionstheorie mit verschiedenen Kombinationen von zwei Inputfaktoren möglich, die bei gleich bleibendem Outputniveau (Produktionsniveau) gegeneinander substituiert werden. Das was in der Haushaltstheorie die Indifferenzkurve abbildet, ist mit der Isoquante in der Produktionstheorie zu vergleichen.

Literatur

• Vilfredo Pareto: Manuale di economia politica, Milano 1906. (keine deutsche Ausgabe, die relevanten Ausführungen Paretos von Kap. III, §§ 52–67 in deutscher Übersetzung in W. Reiß, Mikroökonomische Theorie, Kap. 5, Oldenbourg Verlag, München 1992, ISBN 3-486-22277-5).
• Hal R. Varian: Grundzüge der Mikroökonomik. Oldenbourg Verlag, 2003, ISBN 3-486-27453-8, Kapitel 3.3.
• J. Schumann, U. Meyer, W. Ströbele: Grundzüge der mikroökonomischen Theorie, 8. Auflage, Springer-Verlag, Berlin-Heidelberg-New York 2007, ISBN 978-3-540-70925-1.

Einzelnachweise

1. ↑ Beweisansatz aus: J. Schumann, U. Meyer, W. Ströbele: Grundzüge der mikroökonomischen Theorie, 8. Auflage, S.55. Hier ausführlicher dargestellt.

Weblinks

• Indifferenzkurven – Artikel bei mikrooekonomie.de
• Die Grenzrate der Substitution Artikel bei mikrooekonomie.de (behandelt Sonderfälle von Indifferenzkurven)
• Indifferenzkurve – Definition im Gabler Wirtschaftslexikon