- Effective Core Potential
-
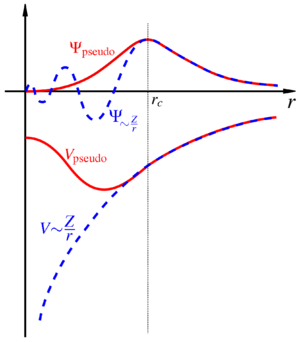
Vergleich einer Wellenfunktion im Coulomb Potential des Nucleus (blau) mit einer im Pseudopotential (rot). Die echte und die Pseudo-Wellenfunktion und die Potentiale selbst stimmen oberhalb des cutoff Radius rc überein.Der Pseudopotential-Formalismus in der Quantenmechanik ist ein Ansatz, um die rechenintensiven kernnahen (nicht Valenz) Elektronen eines Atoms bzw. Ions und den Atomkern durch ein effektives Potential anzunähern. Normalerweise haben die kernnahen Elektronen die höchste Energie, was eine kurze Wellenlänge bedeutet, wodurch mit einer hohen Ortsauflösung gerechnet werden muss. Durch geschickte Wahl eines empirischen Potentials lässt sich der Aufwand zum Lösen der Schrödingergleichung massiv reduzieren. Die Wellenfunktion der Valenzelektronen ist dann orthogonal zu allen Kernzuständen.
Inhaltsverzeichnis
Näherungen
- Ein Ein-Elektron Bild wird benutzt, um Elektronen in Kern- und Valenz-Satz aufzuteilen.
- Frozen-Core Approximation (eingefrorener Kern Näherung): Die Ein-Elektron Zustände des Kernanteils sind konstant.
- Die Small-Core Appr. (kleiner Kern Näherung) nimmt an, dass die Kern- und Valenzzustände keine signifikante Überlappung haben, und damit für das Austausch-Korrelations-Potenzial( siehe DFT(QM)) gilt: Exc(nkern + nvalenz) = Exc(nkern) + Exc(nvalenz); Dies stimmt nicht immer, und dann kann die non-linear core corrections Technik (Louie et al., 1982) zum Verbessern der Ergebnisse verwendet werden.
Arten
Es werden zwei Klassen von Pseudopotentialen verwendet: Norm-conserving PP und Ultrasoft PP.
Norm-conserving (Norm-Erhaltend) PP: Außerhalb eines bestimmten Radius (cutoff-radius) sind die PP-Wellenfunktionen identisch mit den echten (all-electron) WF.
z. B. BHS-PP, Bachelet, Hamann, Schlüter (Hamann et al., 1982)Ultrasoft PP wurden von David Vanderbilt eingeführt [Phys. Rev. B 41,7892, (1990)] und haben den Vorteil, dass die Wellenfunktionen noch „glatter“ sind, also für die gleiche Genauigkeit eine deutlich geringere Anzahl an ebenen Wellen zur Beschreibung benötigen, und somit die Rechenzeit noch geringer ist. Ein Nachteil dieser Potentiale ist aber, dass die Atomorbitale kein Orthonormalsystem mehr bilden.
Beide Arten von Pseudopotentialen sind „nicht-lokal“, das heißt, dass das Potential von der Drehimpulsquantenzahl l abhängt.
Literatur
Harrison (1966), Brust (1968), Stoneham (1975), Heine (1970), Pickett (1989),..
Siehe auch
Wikimedia Foundation.
