Elkies

Noam Elkies 2005

Noam Elkies 2007

Noam D. Elkies (* 25. August 1966 in New York City) ist ein israelisch-amerikanischer Mathematiker, der sich mit Zahlentheorie und Kombinatorik beschäftigt.

Leben

Elkies gewann noch als Vordiplom-Student (Undergraduate) dreimal die Putnam Fellowship, zuerst 1982 mit nur 16 Jahren. Er promovierte 1987 in Harvard bei Barry Mazur und Benedict Gross mit Supersingular primes of a given elliptic curve over a number field. 1990 wurde er Assistenzprofessor in Harvard, wo er 1993 eine volle Professur erhielt (mit 27 Jahren, wodurch er den vorherigen Rekord des Anwalts Alan Dershowitz einstellte).

Mathematik

In seiner Dissertation bewies er, dass es zu jeder elliptischen Kurve E über den rationalen Zahlen unendlich viele supersinguläre Primzahlen gibt („supersingulär“ heißt in diesem Fall, dass die Anzahl der Punkte von E modulo p betrachtet, also über dem endlichen Körper 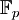$\mathbb F_p$, kongruent zu 1 mod p ist).

1988 gab er ein Gegenbeispiel für eine Vermutung von Euler über Potenzsummen ganzer Zahlen. Dieser behauptete, dass falls

$\sum_{i=1}^{n} a_i^k = b^k$

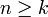$n\geq k$ sein müsste. Lander und Parkin hatten schon 1966 ein Gegenbeispiel für k=5 gegeben, Elkies gab eines für k=4 (1988 fand Roger Frye mit Computermethoden, die auf Elkies Arbeit beruhen, eine kleinere Lösung).

Elkies arbeitete auch über numerisch/algorithmische Probleme der Zahlentheorie elliptischer Kurven, wichtig insbesondere für kryptographische Anwendungen. Mit A. O. L. Atkin verbesserte er den Algorithmus von Rene Schoof zur Bestimmung der Anzahl rationaler Punkte auf elliptischen Kurven.

Elkies ist ein Puzzle-Fan und arbeitete auch auf dem Gebiet kombinatorischer Spiele. Weiter ist er bekannt für die Entdeckung vieler neuer Konfigurationen in John Conways Spiel Life. Auf dem Gebiet der Kombinatorik arbeitete er u.a. über Gitterpackungen und Codes.

Schach

Elkies ist ein aktiver Studienkomponist und starker Löser von Schachkompositionen. Er hat mehr als 40 Schachstudien komponiert. 1996 wurde er in Tel Aviv Weltmeister im Lösen von Schachaufgaben und Studien.

Im Turnierschach hat er die US-Meisterschaft gewonnen.

Noam Elkies
Internet Mailing Liste, 2004

a b c d e f g h 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 a b c d e f g h

Wer gewinnt?

Lösung:

Um die Frage unter dem Diagramm beantworten zu können, ist mit einer Retroanalyse die Entstehungsgeschichte der gezeigten Stellung aufzuklären.

Weiß steht im Schach und anscheinend ist es Schachmatt. In diesem Fall hätte Schwarz gewonnen. Da der schwarze Bauer Schach bietet und der weiße König nicht flüchten kann, kann diesem Schach nur durch Schlagen des Bauers begegnet werden. Dieser Bauer jedoch könnte lediglich en passant durch den weißen Bauern f5 geschlagen werden. In diesem Fall wäre Schwarz matt und Weiß hätte gewonnen.

Notwendige Voraussetzung für das en passant-Schlagen ist der Doppelschritt des zu schlagenden Bauers im unmittelbar vorausgehenden Zug. Wegen des Schachgebots muss der g-Bauer zuletzt gezogen haben. Der Partieausgang hängt davon ab, ob der Bauer von g7 oder von g6 nach g5 gezogen hat.

Diese Frage kann eindeutig entschieden werden, indem der letzte Zug von Weiß ermittelt wird.

Musik

Elkies komponiert Musik und spielt auf dem Piano, seit er drei Jahre alt ist. Er interessiert sich dabei für Anwendungen der Mathematik in der Musik. Einige seiner Stücke wurden auf Radiosendern in Israel und den Vereinigten Staaten ausgestrahlt.

Weblinks

• Homepage, mit Preprints
• Webseite zu Elkies Schachproblemen, holländisch, weitere Schachprobleme von Elkies [1]
• Elkies The Existence of infinitely man supersingular primes for every elliptic curve over Q, Inv. Math. 1987
• Noam Elkies auf einer Schiffstour zum Berg Athos während des 47. PCCC-Kongresses 2004 in Chalkidiki (Griechenland)
• Kompositionen von Noam Elkies auf dem PDB-Server

Großmeister der PCCC im Lösen von Schachkompositionen

1982 | Perkonoja | 1984 | Valtonen | Velimirović | 1985 | Comay | 1988 | Baier | Kovačević | Petkow | A. Zude | Evsejev | 1993 | Pfannkuche | 1997 | Mestel | Rumyantsev | 1998 | Soffer | 1999 | Paavilainen | 2000 | Tummes | 2001 | Elkies | 2002 | Caillaud | Lee | Murdzia | 2004 | Nunn | Wissmann | 2007 | Azhusin | 2008 | Mladenović | Seliwanow | Vučković |

 

Personendaten
NAME	Elkies, Noam
KURZBESCHREIBUNG	US-amerikanischer Mathematiker und Schachkomponist
GEBURTSDATUM	25. August 1966
GEBURTSORT	New York City