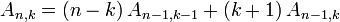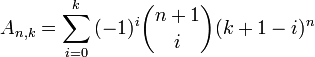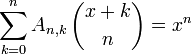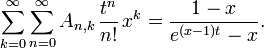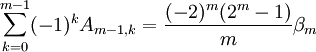Euler-Dreieck

Euler-Zahlen als Koeffizienten von Euler-Polynomen

Die nach Leonhard Euler benannte Euler-Zahl A_n,k in der Kombinatorik, auch geschrieben als E(n,k) oder 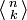$\left\langle\begin{smallmatrix} n \\ k \end{smallmatrix}\right\rangle$, gibt die Anzahl der Permutationen (Anordnungen) von 1, …, n an, in denen genau k Elemente größer als das vorhergehende sind, die also genau k Anstiege enthalten. Äquivalent dazu ist die Definition mit „kleiner“ statt „größer“ und „Abstiege“ statt „Anstiege“. Nach einer anderen Definition sind die Euler-Zahlen a(n,k) die Anzahlen der Permutationen von 1, …, n mit genau k maximalen monoton ansteigenden Abschnitten, wodurch der zweite Parameter gegenüber der hier verwendeten Definition um eins verschoben ist: a(n,k) = A_n,k−1.

Euler-Dreieck

Wie die Binomialkoeffizienten im Pascalschen Dreieck können die Euler-Zahlen im Euler-Dreieck angeordnet werden (erste Zeile n = 1, erste Spalte k = 0):

                             1
                          1     1
                       1     4     1
                    1    11    11     1
                 1    26    66    26     1
              1    57    302   302   57     1
           1    120  1191  2416  1191   120    1
        1    ...   ...   ...   ...   ...   ...    1

Dabei kann man mit der folgenden Rekursionsformel jeden Eintrag aus den beiden darüberstehenden berechnen:

$A_{n,k} = (n-k)\,A_{n-1,k-1} + (k+1)\,A_{n-1,k}$

für n > 0 mit A_0,0 = 1 und A_0,k = 0 für k > 0.

Eigenschaften

Direkt aus der Definition folgen A_n,0 = 1 für n ≥ 0 und A_n,n−1−k = A_n,k für n > 0, k ≥ 0 und

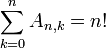$\sum_{k=0}^n A_{n,k} = n!$      für n ≥ 0.

Aus den Binomialkoeffizienten können die Euler-Zahlen mit der Formel

$A_{n,k} = \sum_{i=0}^k\,(-1)^i \binom{n+1}{i} (k+1-i)^n$

für n, k ≥ 0 berechnet werden, insbesondere ist

A_n,1 = 2ⁿ − (n + 1)      und      $A_{n,2} = 3^n - 2^n\,(n+1) + \tfrac12\,n\,(n+1).$

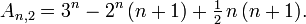
Es gilt die Worpitzky-Identität (nach Julius Worpitzky)

$\sum_{k=0}^n A_{n,k}\,\binom{x+k}{n} = x^n$

für n ≥ 0, wobei x eine Variable und 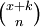$\tbinom{x+k}{n}$ ein verallgemeinerter Binomialkoeffizient ist.

Eine erzeugende Funktion für A_n,k in den Variablen t und x ist

$\sum_{k=0}^\infty \sum_{n=0}^\infty A_{n,k}\,\frac{t^n}{n!}\,x^k = \frac{1-x}{e^{(x-1) t} - x}.$

Eine Beziehung zu den Bernoulli-Zahlen β_m wird durch die alternierende Summe

$\sum_{k=0}^{m-1} (-1)^k A_{m-1,k} = \frac{(-2)^m (2^m - 1)}{m} \beta_m$

für m > 0 hergestellt.

Literatur

• Martin Aigner: Diskrete Mathematik, Vieweg-Verlag, Braunschweig/Wiesbaden 2006, ISBN 978-3-8348-0084-8
• Kenneth H. Rosen, John G. Michaels et al.: Handbook of Discrete and Combinatorial Mathematics, CRC Press LLC, 1999, ISBN 978-0-8493-0149-0 (englisch)
• Julius Worpitzky: Studien über die Bernoullischen und Eulerschen Zahlen, Crelles Journal 94, 1883, S. 203–232

Weblinks

• Eric W. Weisstein: Eulerian Number auf MathWorld (englisch)
• Eric W. Weisstein: Euler’s Number Triangle auf MathWorld (englisch)
• Eric W. Weisstein: Worpitzky’s Identity auf MathWorld (englisch)
• Folge A008292 in OEIS (englisch)