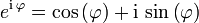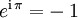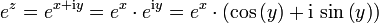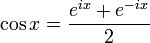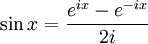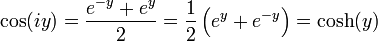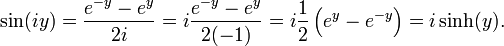Eulerformel

Veranschaulichung in der komplexen Zahlenebene

Die eulersche Identität bezeichnet die Formel

$e^{\mathrm{i}\,\varphi} = \cos\left(\varphi \right) + \mathrm{i}\,\sin\left( \varphi\right)$

und bildet das Bindeglied zwischen trigonometrischen Funktionen und den komplexen Zahlen. Dabei bezeichnet e die eulersche Zahl (Basis des natürlichen Logarithmus) und i die imaginäre Einheit der komplexen Zahlen.

Die Gleichung erscheint in Leonhard Eulers Introductio, veröffentlicht in Lausanne 1748 unter der Voraussetzung 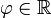$\varphi\in\Bbb R$ (aus der Anschauung wird klar, dass $\varphi$ auch Winkel genannt wird), sie gilt jedoch auch für alle komplexen Argumente $\varphi\in\Bbb C$.

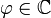Für den Winkel 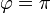$\varphi = \pi$ (die Kreiszahl; entspricht einem Winkel von 180°) ergibt sich die Identität

$\begin{matrix} e^{\mathrm{i}\,\pi} = \end{matrix}-1\;$

die einen verblüffend einfachen Zusammenhang zwischen vier der bedeutendsten mathematischen Konstanten herstellt: der eulerschen Zahl e, der imaginären Einheit i der komplexen Zahlen, der Kreiszahl 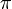$\pi\,$ sowie der Einheit 1 der reellen Zahlen.

Eine alternative, ebenfalls weit verbreitete Schreibweise der Gleichung lautet:

$\begin{matrix} e^{\mathrm{i}\,\pi}\end{matrix}+1=0\;$.

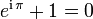Anwendungen

Bei der Berechnung der Potenz iⁱ der imaginären Einheit mit sich selbst wird die eulersche Identität benutzt, siehe Potenz (Mathematik). Der Potenzausdruck ist mehrdeutig; die Lösungen sind aber alle reell mit dem Hauptwert $\mathrm{i}^\mathrm{i}\approx 0{,}207\,879\,576\,350\,762$.

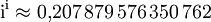Eulersche Formel

Als einfache Folgerung der eulerschen Identität erhält man die eulersche Formel, die sich folgendermaßen darstellt:

$e^z = e^{x+\mathrm{i}y} = e^x \cdot e^{\mathrm{i}y} = e^x \cdot \left(\cos\left( y \right) + \mathrm{i}\,\sin\left( y \right)\right)$

Hieraus erhält man sofort eine Darstellung des Betrages von e^z: | e^z | = e^x.

Verbindung der Analysis zur Trigonometrie

Die Eulerformel dient als Bindeglied zwischen Analysis und Trigonometrie, da die trigonometrischen Funktionen als Linearkombinationen von imaginären Exponentialfunktionen dargestellt werden können:

$\cos x = {e^{ix} + e^{-ix} \over 2}$

$\sin x = {e^{ix} - e^{-ix} \over 2i}$

Damit wird eine neue Interpretation der trigonometrischen Funktionen ermöglicht. Die im Rahmen der Trigonometrie verwendeten rein reellen Funktionen Sinus und Kosinus besitzen nun auch Bedeutung in der komplexen Analysis.

Es ist nun möglich, die trigonometrischen Funktionen ihrerseits mit (rein) imaginären Argumenten zu versehen:

$\cos(iy) = {e^{-y} + e^{y} \over 2} = \frac{1}{2} \left( e^y + e^{-y} \right) = \cosh(y)$

und

$\sin(iy) = {e^{-y} - e^{y} \over 2i} = i {e^{-y} - e^{y} \over 2(-1)} = i \frac{1}{2} \left( e^y - e^{-y} \right) = i \sinh(y) .$

Beide Funktionen entsprechen gerade der Definition der Hyperbelfunktionen.