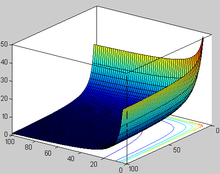
- Eulersche Betafunktion
-
Die Eulersche Betafunktion, auch Eulersches Integral 1. Art (nach Leonhard Euler) ist eine mathematische Funktion zweier komplexer Zahlen, die mit Β bezeichnet wird. Ihre Definition lautet:
wobei x und y einen positiven Realteil haben müssen.
Die Betafunktion war die erste bekannte Streuamplitude in der Stringtheorie. Sie tritt darüber hinaus bei der Betaverteilung auf.
Inhaltsverzeichnis
Allgemeines
Bei festem x (bzw. y) ist Β eine holomorphe Funktion von y (bzw. x), und für die Funktion gilt die Symmetrierelation
- Β(x,y) = Β(y,x).
Es existieren folgende weitere Integraldarstellungen für die Betafunktion mit Re(x) > 0 und Re(y) > 0
Das Hauptresultat der Theorie der Betafunktion ist die Identität
wobei Γ die Eulersche Gammafunktion bezeichnet. An dieser Darstellung kann man auch ablesen, dass die analytische Fortsetzung der Betafunktion Pole genau entlang x = k und y = k für ganze Zahlen
 hat.
hat.Theodor Schneider zeigte 1940, dass Β(x,y) für alle rationalen, nicht ganzzahligen x, y transzendent ist.[1]
Darstellungen
Die Betafunktion hat viele weitere Darstellungen wie:
Die Betafunktion kann, durch Anpassen der Indizes, zur Definition der Binomialkoeffizienten verwendet werden:
Mit der Darstellung für die Gammafunktion kommt man für ganzzahlige x und y auf:
 .
.
Ableitung
Die Ableitung ist gegeben durch
wobei ψ(x) die Digamma-Funktion ist.
Einzelnachweise
- ↑ Theodor Schneider: Zur Theorie der Abelschen Funktionen und Integrale (22. Januar 1940), Journal für die reine und angewandte Mathematik 183, 1941, S. 110–128 (beim GDZ: [1])
Weblinks
- Eric W. Weisstein: Beta Function, Regularized Beta Function, Incomplete Beta Function in MathWorld (englisch)
- Beta function. Evaluation bei functions.wolfram.com (englisch)
Wikimedia Foundation.