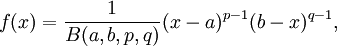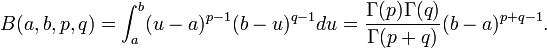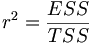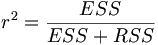- Beta-Verteilung
-
Die Betaverteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung über dem Intervall [0,1].
Inhaltsverzeichnis
Definition
Betaverteilung auf [0,1]
Die Betaverteilung ist definiert durch die Wahrscheinlichkeitsdichte
Außerhalb des Intervalls [0,1] wird sie durch f(x) = 0 fortgesetzt. Sie besitzt die Parameter p und q. Um ihre Normierbarkeit zu garantieren, wird p,q > 0 gefordert.
Der Vorfaktor 1 / B(p,q) dient der korrekten Normierung. Der Ausdruck
steht für die Betafunktion, nach der die Verteilung benannt ist. Dabei bezeichnet Γ die Gammafunktion.
Die Verteilungsfunktion ist entsprechend
diese Funktion heißt auch regularisierte unvollständige Betafunktion.
Betaverteilung auf [a,b]
Die allgemeine Betaverteilung ist definiert zu
wobei a und b die obere und untere Grenze des Intervalls sind. Entsprechend ergibt sich die Berechnung von B zu
Die weiteren Ausführungen in diesem Artikel beziehen sich nur auf die auf das Intervall [0,1] eingeschränkte Betaverteilung.
Eigenschaften
Extremum
Die Dichtefunktion f nimmt ihr Extremum an der Stelle
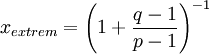 an.
an.Erwartungswert
Der Erwartungswert berechnet sich zu
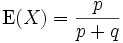 .
.
Varianz
Die Varianz ergibt sich zu
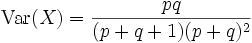 .
.
Standardabweichung
Für die Standardabweichung ergibt sich
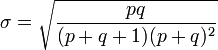 .
.
Variationskoeffizient
Aus Erwartungswert und Varianz erhält man unmittelbar den Variationskoeffizienten
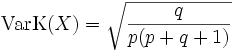 .
.
Schiefe
Die Schiefe ergibt sich zu
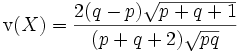 .
.
Symmetrie
Die Beta-Verteilung ist für p = q symmetrisch um
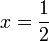 mit der Schiefe
mit der Schiefe 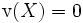 .
.Beziehungen zu anderen Verteilungen
Beziehung zur F-Verteilung
Wenn
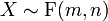 F-verteilt und
F-verteilt und 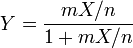 ist, dann verteilt sich
ist, dann verteilt sich 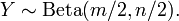
Beziehung zur Gammaverteilung
Wenn die Zufallsvariablen X mit γ(a1,b)und Y mit γ(a2,b) Gamma-verteilt sind mit den Parametern a1,a2 und b, dann ist die Größe
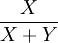 Beta-verteilt mit
Beta-verteilt mit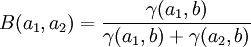 .
.
Beispiel
Die Betaverteilung kann aus zwei Gammaverteilungen erhalten werden: Der Quotient X = U / (U + V) aus den stochastisch unabhängigen Zufallsvariablen U und V, die beide gammaverteilt sind mit den Parametern b und pu bzw. pv, ist betaverteilt mit den Parametern pu und pv. U und V lassen sich als Chi-Quadrat-Verteilungen mit 2pu bzw. 2pv Freiheitsgraden interpretieren.
Mit Hilfe der Linearen Regression wird eine Regressionsgerade y = a + bx durch eine Punktwolke mit n Wertepaaren
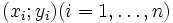 zweier statistischer Merkmale x und y gelegt, und zwar so, dass die Quadratsumme der senkrechten Abstände der yi-Werte von der Geraden minimiert wird.
zweier statistischer Merkmale x und y gelegt, und zwar so, dass die Quadratsumme der senkrechten Abstände der yi-Werte von der Geraden minimiert wird.Die totale Streuung von y (TSS) lässt sich mit der Streuungszerlegung zerlegen in die so genannte erklärte Streuung der durch die Gerade geschätzten Werte y* (ESS) und die nichterklärte Streuung der Residuen (RSS):
- TSS = ESS + RSS.
Das Bestimmtheitsmaß, der Anteil der erklärten Streuung an der Gesamtstreuung
beziehungsweise
ist also betaverteilt. Da das Bestimmtheitsmaß das Quadrat des Korrelationskoeffizienten von x und y darstellt, ist auch das Quadrat des Korrelationskoeffizienten betaverteilt.
Allerdings kann die Verteilung des Bestimmtheitsmaßes beim Modelltest der Regression durch die F-Verteilung angegeben werden, die tabelliert vorliegt.
Weblinks
- Universität Konstanz – Interaktive Animation
Diskrete univariate VerteilungenDiskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-MandelbrotDiskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | ZetaKontinuierliche univariate VerteilungenKontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-HalbkreisKontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambdaKontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | VoigtMultivariate VerteilungenDiskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet MultinomialKontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-GammaMultivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart
Wikimedia Foundation.

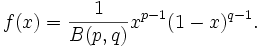
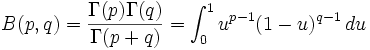
![F(x)=\frac{\mathbb{I}_{[0,1]}(x)}{B(p,q)}\cdot \int_0^{x} u^{p-1} (1-u)^{q-1}\mathrm{d}u,](/pictures/dewiki/50/2044350147003e7ef165f67eda972224.png)