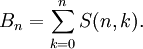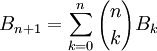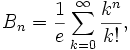Exponentialzahl

Die Bellsche Zahl, Bellzahl oder Exponentialzahl B_n ist die Anzahl der Partitionen einer n-elementigen Menge. Benannt ist sie nach dem Mathematiker Eric Temple Bell. Es ist

$B_0=1, \quad B_1=1, \quad B_2=2, \quad B_3=5, \quad B_4=15, \quad B_5=52, \quad B_6=203, \quad \ldots$

Eigenschaften

Da die Stirling-Zahl S(n,k) zweiter Art die Anzahl der k-Partitionen einer n-elementigen Menge ist, gilt

$B_n = \sum_{k=0}^n S(n,k).$

Für die Bellschen Zahlen gelten die Rekursionsformel

$B_{n+1} = \sum_{k=0}^{n}{{n \choose k}B_k}$

und Dobińskis Formel

$B_n = \frac{1}{e}\sum_{k=0}^\infty \frac{k^n}{k!},$

somit ist B_n auch das n-te Moment einer Poissonverteilung mit Erwartungswert 1.

Die exponentiell erzeugende Funktion der Bellzahlen ist $\sum_{n=0}^\infty \frac{B_n}{n!} x^n = e^{e^x-1}.$

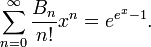
Außerdem genügen die Bellzahlen Touchards Kongruenz:

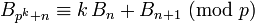$B_{p^k+n} \equiv k\,B_n + B_{n+1}\ (\operatorname{mod}\ p)$     für natürliche Zahlen k und Primzahlen p.

Insbesondere gelten 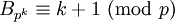$B_{p^k} \equiv k + 1\ (\operatorname{mod}\ p)$ und $B_p \equiv 2\ (\operatorname{mod}\ p)$.

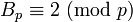Asymptotik

Für die Bellzahlen sind verschiedene asymptotische Formeln bekannt, etwa

$B_n \sim n^{-1/2}\ \bigl(\lambda(n)\bigr)^{n + 1/2}\ e^{\lambda(n) - n - 1}$     mit     $\lambda(n) = e^{W(n)} = \frac{n}{W(n)}$

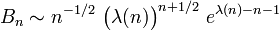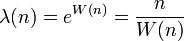
mit der Lambert-W-Funktion W.

Literatur

• G. Dobiński: Summirung der Reihe Σ n^m/ n! für m = 1, 2, 3, 4, 5, …, Grunert-Archiv 61, 1877, S. 333–336 (im Internet-Archiv: [1])
• Jacques Touchard: Propriétés arithmétiques de certains nombres récurrents, Annales de la Société scientifique de Bruxelles 53, 1933, S. 21–31 (französisch)
• Eric Temple Bell: Exponential Numbers, The American Mathematical Monthly 41, 1934, S. 411–419
• Jacques Touchard: Nombres exponentiels et nombres de Bernoulli, Canadian Journal of Mathematics 8, 1956, S. 305–320 (französisch)

Weblinks

• Eric W. Weisstein: Bell Number auf MathWorld (englisch)
• Eric W. Weisstein: Dobiński’s Formula auf MathWorld (englisch)
• Folge A000110 in OEIS (englisch)