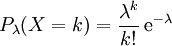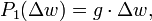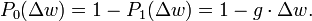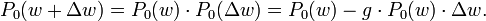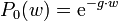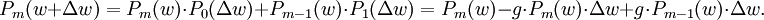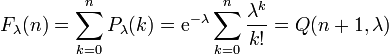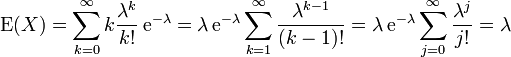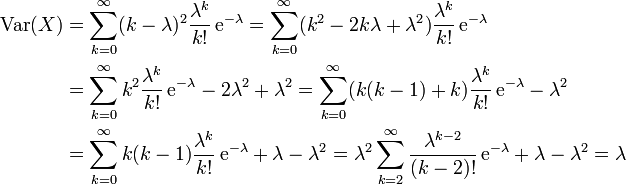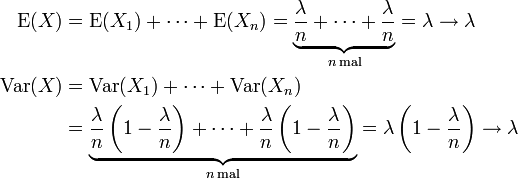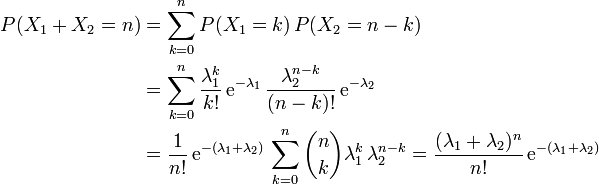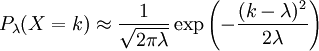- Poissonverteilung
-
Die Poisson-Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung, die beim mehrmaligen Durchführen eines Bernoulli-Experiments entsteht. Letzteres ist ein Zufallsexperiment, das nur zwei mögliche Ergebnisse besitzt (z. B. „Erfolg“ und „Misserfolg“). Führt man ein solches Experiment sehr oft durch und ist die Erfolgswahrscheinlichkeit gering, so ist die Poisson-Verteilung eine gute Näherung für die entsprechende Wahrscheinlichkeitsverteilung. Die Poisson-Verteilung wird deshalb manchmal als die Verteilung der seltenen Ereignisse bezeichnet (siehe auch Gesetz der kleinen Zahlen). Zufallsvariablen mit einer Poisson-Verteilung genügen dem Poisson-Prozess.
Die mit Pλ bezeichnete Wahrscheinlichkeitsverteilung wird durch den Parameter λ bestimmt, der gleichzeitig Erwartungswert und Varianz der Verteilung ist. Sie ordnet den natürlichen Zahlen
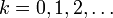 die Wahrscheinlichkeiten wie folgt zu:
die Wahrscheinlichkeiten wie folgt zu:wobei
- e die Eulersche Zahl (Exponentialfunktion)
- λ eine reelle positive Zahl
- k! die Fakultät von k
bezeichnen.
Die Poisson-Verteilung liefert also Voraussagen über die Anzahl (k) des Eintretens seltener, zufälliger und voneinander unabhängiger Ereignisse innerhalb eines bestimmten Intervalls, wenn aus vorangehender Beobachtung bereits bekannt ist, wie viele Ereignisse man im Mittel innerhalb dieses Intervalls erwartet (λ). Sie ist ein Spezialfall der Panjer-Verteilung.
Siméon Denis Poisson veröffentlichte 1837 seine Gedanken zu dieser Verteilung zusammen mit seiner Wahrscheinlichkeitstheorie in dem Werk „Recherches sur la probabilité des jugements en matières criminelles et en matière civile“ („Untersuchungen zur Wahrscheinlichkeit von Urteilen in Straf- und Zivilsachen“).
Erweiterungen der Poisson-Verteilung wie die Verallgemeinerte Poisson-Verteilung und die Gemischte Poisson-Verteilung werden vor allem im Bereich der Versicherungsmathematik angewandt.
Inhaltsverzeichnis
- 1 Herleitung
- 2 Eigenschaften
- 3 Beziehung zu anderen Verteilungen
- 4 Anwendungsbeispiele
- 5 Zufallszahlen
- 6 Literatur
- 7 Weblinks
Herleitung
Die Poisson-Verteilung ergibt sich einerseits als Grenzfall der Binomial-Verteilung, andererseits lässt sie sich aus grundlegenden Prozesseigenschaften (poissonsche Annahmen) ableiten. Wenn diese Eigenschaften einem Geschehen in guter Näherung zugeordnet werden können, wird die Ereignishäufigkeit Poisson-verteilt sein.
Man betrachtet ein Raum- oder Zeitkontinuum w (das Bernoulli-Experiment wird sehr oft, sozusagen an jedem Punkt des Kontinuums durchgeführt), 'auf' dem zählbare Ereignisse mit konstanter mittlerer Anzahl g pro Einheitsintervall stattfinden. Nun richtet man den Blick auf ein 'genügend' kleines Kontinuumsintervall Δw, das je nach Experiment einen Bereich, ein Zeitintervall, eine abgegrenzte Strecke, Fläche oder Volumen darstellen kann. Was sich dort ereignet, bestimmt die globale Verteilung auf dem Kontiunuum.
Die drei poissonschen Annahmen lauten:
- Innerhalb des Intervalls [w,w + Δw] gibt es höchstens ein Ereignis (Seltenheit).
- Die Wahrscheinlichkeit, ein Ereignis im Intervall zu finden, ist proportional zur Länge des Intervalls Δw (g ist konstant und damit auch unabhängig von w).
- Das Eintreten eines Ereignisses im Intervall Δw wird nicht beeinflusst von Ereignissen, die in der Vorgeschichte stattgefunden haben (Geschichtslosigkeit).
Mit Annahme 1 und 2 ist die Wahrscheinlichkeit, ein Ereignis im Intervall Δw zu finden, gegeben durch
sowie die Wahrscheinlichkeit eines leeren Intervalls durch
Nach Annahme 3 ist die Wahrscheinlichkeit eines leeren Intervalls Δw unabhängig vom Auftreten irgendwelcher Ereignisse im Bereich w davor. So berechnet man die Wahrscheinlichkeit für kein Ereignis bis zum Punkt w + Δw zu
Das ergibt näherungsweise die Differentialgleichung
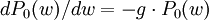 mit der Lösung
mit der Lösungunter der Randbedingung P0(0) = 1. Ebenso findet man die Wahrscheinlichkeit für m Ereignisse bis zum Punkt w + Δw
Jedes drangehängte Intervall Δw darf nach Annahme 1 nur entweder kein oder ein Ereignis enthalten. Die entsprechende Differentialgleichung
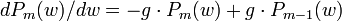 hat die Lösung
hat die Lösung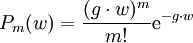 .
.
Identifiziert man nun in diesem Ausdruck für die Wahrscheinlichkeit des Eintretens von m Ereignissen im Kontinuumsbereich w die Parameter
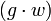 mit λ und m mit k, stimmt er mit der Formel der Poisson-Verteilung überein. Die Zahl λ ergibt sich in vielen Aufgabenstellungen als Produkt einer Rate (Anzahl von Ereignissen pro Einheitsintervall) und einem Vielfachen des Einheitsintervalls.
mit λ und m mit k, stimmt er mit der Formel der Poisson-Verteilung überein. Die Zahl λ ergibt sich in vielen Aufgabenstellungen als Produkt einer Rate (Anzahl von Ereignissen pro Einheitsintervall) und einem Vielfachen des Einheitsintervalls.Eigenschaften
- Die Poisson-Verteilung Pλ wird durch den Parameter λ vollständig charakterisiert.
- Die Poisson-Verteilung ist stationär, d. h. nicht von der Zeit abhängig.
- In einem Poisson-Prozess ist die zufällige Anzahl der Ereignisse bis zu einem bestimmten Zeitpunkt Poisson-verteilt, die zufällige Zeit bis zum n-ten Ereignis Erlang-verteilt. Wichtig ist der Spezialfall n = 0, der zur Exponentialverteilung führt. Sie beschreibt die Zeit bis zum ersten zufälligen Ereignis (sowie die Zeit zwischen zwei aufeinanderfolgenden Ereignissen) eines Poissonprozesses.
Einfache rekursive Berechnung
Zuerst bestimmt man Pλ(0) = e − λ, dann ergeben sich nacheinander
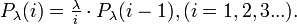 Mit wachsendem i werden dabei die Wahrscheinlichkeiten grösser, solange i < λ ist. Wird i > λ, schrumpfen sie.
Mit wachsendem i werden dabei die Wahrscheinlichkeiten grösser, solange i < λ ist. Wird i > λ, schrumpfen sie.Verteilungsfunktion
Die Verteilungsfunktion F(x) der Poisson-Verteilung lautet
und gibt die Wahrscheinlichkeit dafür, höchstens n Ereignisse zu finden, wo man λ im Mittel erwartet. Q(a,x) ist die regularisierte Gammafunktion der unteren Grenze.
Erwartungswert, Varianz, Moment
λ ist zugleich Erwartungswert, Varianz und auch 3. zentriertes Moment
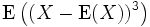 , denn
, dennErwartungswert
Varianz
Alternative Berechnung von Erwartungswert und Varianz
Seien
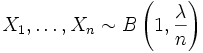 unabhängige binomialverteilte Zufallsvariablen und sei
unabhängige binomialverteilte Zufallsvariablen und sei 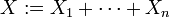 . Für
. Für 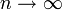 gilt
gilt 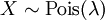 .
.Variationskoeffizient
Aus Erwartungswert und Varianz erhält man sofort den Variationskoeffizienten
 .
.
Schiefe und Wölbung
Die Schiefe ergibt sich zu
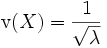 .
.
Die Wölbung lässt sich ebenfalls geschlossen darstellen als
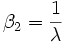 .
.
Charakteristische Funktion
Die charakteristische Funktion hat die Form
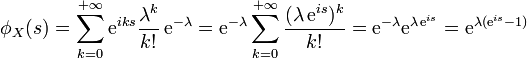 .
.
Erzeugende Funktion
Für die erzeugende Funktion erhält man
- gX(s) = eλ(s − 1).
Momenterzeugende Funktion
Die momenterzeugende Funktion der Poisson-Verteilung ist
 .
.
Reproduktivität
Die Poisson-Verteilung ist reproduktiv, d.h. die Summe X1 + X2 zweier stochastisch unabhängiger Poisson-verteilter Zufallsvariablen X1 und X2 mit den Parametern λ1 und λ2 ist wieder Poisson-verteilt mit dem Parameter λ1 + λ2. Denn es gilt:
Dies lässt sich auch auf mehrere stochastisch unabhängige poissonverteilte Zufallsvariablen
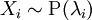 verallgemeinern. Hier ist
verallgemeinern. Hier ist 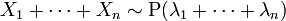 .
.Nach einem Satz des sowjetischen Mathematiker D. A. Raikow gilt auch die Umkehrung: Ist eine Poisson-verteilte Zufallsvariable X die Summe von zwei unabhängigen Zufallsvariablen X1 und X2, dann sind die Summanden X1 und X2 ebenfalls Poisson-verteilt. Eine Poisson-verteilte Zufallsvariable lässt sich also nur in Poisson-verteilte unabhängige Summanden zerlegen. Dieser Satz ist ein Analogon zu dem Satz von Cramér für die Normalverteilung.
Die Poisson-Verteilung ist unendlich teilbar.
Symmetrie
Die Poisson-Verteilung Pλ hat für kleine Mittelwerte λ eine stark asymmetrische Gestalt. Für größer werdende Mittelwerte wird Pλ symmetrischer und lässt sich für λ > 30 in guter Näherung durch die Gauß-Verteilung darstellen.
Beziehung zu anderen Verteilungen
Beziehung zur Binomialverteilung
Die Poisson-Verteilung lässt sich aus der Binomialverteilung
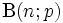 herleiten. Sie ist die Grenzverteilung der Binomialverteilung bei sehr kleinen Anteilen der interessierten Merkmale und sehr großem Stichprobenumfang:
herleiten. Sie ist die Grenzverteilung der Binomialverteilung bei sehr kleinen Anteilen der interessierten Merkmale und sehr großem Stichprobenumfang: 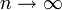 und
und  unter der Nebenbedingung, dass das Produkt np = λ konstant ist. λ ist dann für alle in der Grenzwertbildung betrachteten Binomialverteilungen wie auch für die resultierende Poisson-Verteilung der Erwartungswert.
unter der Nebenbedingung, dass das Produkt np = λ konstant ist. λ ist dann für alle in der Grenzwertbildung betrachteten Binomialverteilungen wie auch für die resultierende Poisson-Verteilung der Erwartungswert.Mit
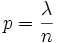 ist der Wert einer Poisson-verteilten Zufallsvariable an der Stelle k der Grenzwert
ist der Wert einer Poisson-verteilten Zufallsvariable an der Stelle k der Grenzwert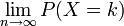
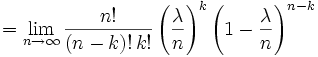
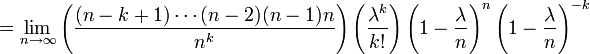
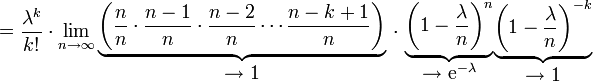
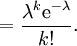
Beziehung zur Normalverteilung
Für große λ kann die Poisson-Verteilung durch die Gaußsche Normalverteilung mit μ = λ und σ2 = λ angenähert werden:
Beziehung zur Erlang-Verteilung
- In einem Poisson-Prozess genügt die zufällige Anzahl der Ereignisse bis zu einem festgelegten Zeitpunkt der Poisson-Verteilung
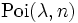 . Die zufällige Zeit bis zum Eintreffen des n-ten Ereignis hingegen ist
. Die zufällige Zeit bis zum Eintreffen des n-ten Ereignis hingegen ist 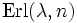 Erlang-verteilt. Im Fall n = 1 geht diese Erlang-Verteilung in eine Exponentialverteilung über
Erlang-verteilt. Im Fall n = 1 geht diese Erlang-Verteilung in eine Exponentialverteilung über 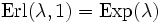 . Man sagt auch, dass die Poisson-Verteilung und die Erlang-Verteilung zueinander konjugierte Verteilungen sind.
. Man sagt auch, dass die Poisson-Verteilung und die Erlang-Verteilung zueinander konjugierte Verteilungen sind. - Für die Verteilungsfunktionen der Erlang-Verteilung und der Poisson-Verteilung gilt
- FErlang(n + 1) + FPoisson(n) = 1.
Beziehung zur Exponentialverteilung
Die Zeit bis zum ersten zufälligen Ereignis sowie die Zeit zwischen zwei aufeinanderfolgenden Ereignissen eines Poisson-Prozesses mit dem Parameter λ ist
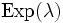 exponentialverteilt.
exponentialverteilt.Anwendungsbeispiele
Die Poisson-Verteilung ist eine typische Verteilung für die Zahl von Phänomenen, die innerhalb einer Einheit auftreten.
So wird sie häufig dazu benutzt, zeitliche Ereignisse zu beschreiben. Gegeben sind ein zufälliges Ereignis, das durchschnittlich einmal in einem zeitlichen Abstand t1 stattfindet, sowie ein zweiter Zeitraum t2, auf den dieses Ereignis bezogen werden soll.
Die Poissonverteilung Pλ(n) mit λ = t2 * 1 / t1 gibt die Wahrscheinlichkeit an, dass im Zeitraum t2 genau n Ereignisse stattfinden. Anders ausgedrückt ist λ die mittlere Auftretenshäufigkeit eines Ereignisses.
Kaufhauskunden
Ein Kaufhaus wird an einem Samstag durchschnittlich alle 10 Sekunden (t1) von einem Kunden betreten. Werden nun im Takt von einer Minute bzw. 60 Sekunden die Personen gezählt, so würde man im Mittel 6 Personen erwarten (λ = 6 Personen/Minute), die das Kaufhaus betreten. P6(n) gibt die Wahrscheinlichkeit dafür an, dass in der nächsten Minute (t2) genau n Kunden das Kaufhaus betreten.
P6(n) n Wahrscheinlichkeit in % Summe in % 0 0,25 0,25 1 1,49 1,74 2 4,46 6,20 3 8,92 15,12 4 13,39 28,51 5 16,06 44,57 6 16,06 60,63 7 13,77 74,40 8 10,33 84,72 9 6,88 91,61 10 4,13 95,74 11 2,25 97,99 12 1,13 99,12 13 0,52 99,64 14 0,22 99,86 15 0,09 99,95 Mit einer Wahrscheinlichkeit von rund 4,5 % betreten genau 2 Personen in einer Minute das Kaufhaus. Mit einer Wahrscheinlichkeit von fast 92 % treten 0 bis 9 Personen (aufsummiert) ein. Die Wahrscheinlichkeit, dass mehr als 9 Personen in einer Minute eintreten, ist folglich 8 %.
Die Werte in der mittleren Spalte ergeben sich jeweils aus dem darüberliegenden Wert, multipliziert mit 6/n.
Radioaktiver Zerfall
In der Natur folgt zum Beispiel die zeitliche Abfolge radioaktiver Zerfälle einzelner Atome der Poisson-Statistik.
Blitzeinschläge
Die Blitzhäufigkeit in Deutschland beträgt 10 Einschläge pro km² = 0,1 Einschläge pro ha und Jahr. Wie groß ist die Wahrscheinlichkeit, dass es in einer Parzelle von 1 ha zu n Blitzeinschlägen in einem Jahr kommt?
λ = 0,1 Einschläge pro Hektar und Jahr.
- P0,1(n = 0) (kein Einschlag im betrachteten Jahr): 90%
- P0,1(n = 1) (ein Einschlag im betrachteten Jahr): 9%
- P0,1(n = 2) (zwei Einschläge im betrachteten Jahr): 0,5%
- P0,1(n = 3) (drei Einschläge im betrachteten Jahr): 0,02%
Statistisch ist es nicht verwunderlich, wenn ein Blitz innerhalb von 200 Jahren zweimal am gleichen Ort einschlägt, wobei es außerordentlich unwahrscheinlich ist, den Ort voraussagen zu können (Siehe hierzu auch Geburtstagsparadoxon).
Verstreute Reiskörner
Das Bild rechts zeigt N = 66 Reiskörner, die zufällig auf n = 49 Quadrate verteilt wurden. Die Felder enthalten
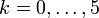 Reiskörner. Der Vergleich zwischen Experiment und berechneter Poissonverteilung P(X = k), wobei λ = N / n = 66 / 49 = 1,33 Reiskörner/Quadrate ist, zeigt eine gute Übereinstimmung:
Reiskörner. Der Vergleich zwischen Experiment und berechneter Poissonverteilung P(X = k), wobei λ = N / n = 66 / 49 = 1,33 Reiskörner/Quadrate ist, zeigt eine gute Übereinstimmung:k gezählt 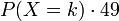
0
16
13
1
14
17
2
10
11
3
6
5
4
1
2
5
2
0,5
Die Wahrscheinlichkeit, dass ein bestimmtes Feld leer bleibt, ist etwas größer als 25%:
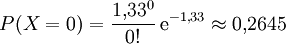
Zufallszahlen
Zufallszahlen zur Poisson-Verteilung werden üblicherweise mit Hilfe der Inversionsmethode erzeugt.
Literatur
- Erich Härtter: Wahrscheinlichkeitsrechnung für Wirtschafts- und Naturwissenschaftler. Vandenhoeck und Ruprecht, Göttingen 1974, ISBN 3-525-03114-9.
- Frodesen, Skjeggestad, Tofte: Probabibility and Statistics in Particle Physics, Universitetsforlaget, Bergen - Oslo - Tromsö
Weblinks
- Universität Konstanz – Interaktive Animation
- StatWiki – Herleitung der momenterzeugenden Funktion
Diskrete univariate VerteilungenDiskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-MandelbrotDiskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | ZetaKontinuierliche univariate VerteilungenKontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-HalbkreisKontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambdaKontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | VoigtMultivariate VerteilungenDiskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet MultinomialKontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-GammaMultivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart
Wikimedia Foundation.