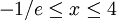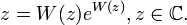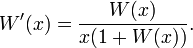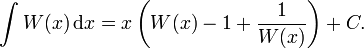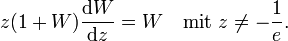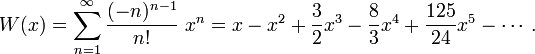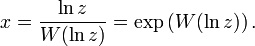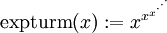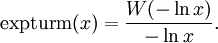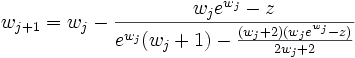Lambert-W-Funktion

Der Graph von W(x) für $-1/e\le x\le 4$

In der Mathematik ist die lambertsche W-Funktion (oder Lambert-W-Funktion), benannt nach Johann Heinrich Lambert, die Umkehrfunktion von

f(x): = xe^x,

wobei e^x die Exponentialfunktion ist. Die lambertsche W-Funktion, auch Omegafunktion genannt, wird meistens mit W(x) bezeichnet. Es gilt

$z = W(z)e^{W(z)}, z\in\mathbb C.$

Eigenschaften

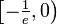Da die Funktion f auf dem Intervall $\left(-\infty,0\right]$ nicht injektiv ist, besitzt die lambertsche W-Funktion auf dem Intervall $\left[-\tfrac 1e,0\right)$ zwei Funktionsäste. Mit W(x) wird aber in der Regel der obere der Äste bezeichnet. Die W-Funktion kann nicht als elementare Funktion ausgedrückt werden. Zumeist wird sie in der Kombinatorik verwendet, z. B. zur Auswertung von Bäumen oder zur asymptotischen Bestimmung der Bell-Zahlen. Die Ableitungsfunktion der W-Funktion kann mit Hilfe des Satzes über die Ableitung der Umkehrfunktion gefunden werden:

$W'(x)=\frac{W(x)}{x(1+W(x))}.$

Eine Stammfunktion ergibt sich durch Substitution des gesamten Integranden:

$\int W(x)\, \mathrm dx = x \left(W(x) - 1 + \frac 1{W(x)} \right) + C.$

Durch implizite Differentiation kann man zeigen, dass W folgender Differentialgleichung genügt:

$z(1+W)\frac{\mathrm dW}{\mathrm dz}=W\quad\text{mit }z\neq -\frac 1e.$

Die Taylor-Reihe von W in x₀ = 0 ist gegeben durch

$W(x) = \sum_{n=1}^\infty \frac{(-n)^{n-1}}{n!}\ x^n = x - x^2 + \frac 32 x^3 - \frac 83 x^4 + \frac{125}{24}x^5 - \dotsb.$

Der Konvergenzradius beträgt $\tfrac 1e$.

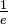Spezielle Werte

$W\left(-\frac{\pi}{2}\right) = \frac{\mathrm i\pi} 2$

$W\left(-\frac 1e\right) = -1$

$W\left(-\frac{\ln 2}{2}\right)= -\ln 2$

$W\left(0\right) = 0$

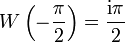
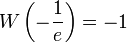
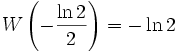
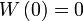
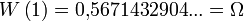$W\left(1\right) = 0{,}5671432904... = \Omega$ (die Omega-Konstante, ((en)))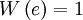

$W\left(e\right) = 1$

Eigenschaften

• $\int_{0}^{\pi} W\left( 2\cot^2(x) \right)\sec^2(x)\,\mathrm dx = 4\sqrt{\pi}$

• $\int_{0}^{+\infty} W\left(\frac{1}{x^2}\right)\,\mathrm dx = \sqrt{2\pi}$

• $\int_{0}^{+\infty} \frac{W(x)}{x\sqrt{x}}\,\mathrm dx = 2\sqrt{2\pi}$

Verwendung außerhalb der Kombinatorik

Die lambertsche W-Funktion kann gebraucht werden, um Gleichungen vom Typus

a(x)e^a(x) = y

zu lösen (a(x) ist ein beliebiger, von x abhängiger Ausdruck).

Auch die Gleichung

x^x = z

kann mit Hilfe der lambertschen W-Funktion gelöst werden. Die Lösung lautet

$x=\frac{\ln z}{W(\ln z)}=\exp\left(W(\ln z)\right).$

Der infinite (unendliche) Potenzturm

$\operatorname{expturm}(x):=x^{x^{x^{\cdot^{\cdot^{\cdot}}}}}$

kann an den konvergenten Stellen mit der W-Funktion in geschlossene Form gebracht werden, was auch die Ableitung ermöglicht:

$\operatorname{expturm}(x)=\frac{W(-\ln x)}{-\ln x}.$

Numerische Berechnung

Die W-Funktion kann rekursiv mithilfe der Beziehung

$w_{j+1}=w_j-\frac{w_j e^{w_j}-z}{e^{w_j}(w_j+1)-\frac{(w_j+2)(w_je^{w_j}-z)}{2w_j+2}}$

berechnet werden^[1].

Einzelnachweise

1. ↑ Corless et al. "On the Lambert W function" Adv. Computational Maths. 5, 329 - 359 (1996)