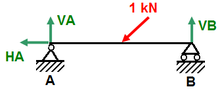
Statisch bestimmt

Ein statisches System (Körper, Tragwerk, Stabtragwerk) ist statisch bestimmt gelagert, wenn die Anzahl seiner Lagerreaktionen (Auflagerbedingungen) der Anzahl seiner Freiheitsgrade entspricht und die Lagerreaktionen allein mit den Gleichgewichtsbedingungen aus der äußeren Belastung berechnet werden können. Das gilt auch für alle Schnittgrößen an beliebigen Teilsystemen.

Alle anderen Systeme sind statisch unbestimmt.

Gleichgewichtsbedingungen

Zur Berechnung aller statisch bestimmten Systeme genügen als Hilfsmittel die Gleichgewichtsbedingungen: Bei ebener Statik die drei Gleichgewichtsbedingungen:

1. Die Summe aller Vertikalkräfte V = 0
2. Die Summe aller Horizontalkräfte H = 0
3. Die Summe aller Momente M = 0

Bei räumlicher Statik ergeben sich analog sechs Gleichgewichtsbedingungen:

1. Summe aller Kräfte in Richtung der x-Achse = 0
2. Summe aller Kräfte in Richtung der y-Achse = 0
3. Summe aller Kräfte in Richtung der z-Achse = 0
4. Summe aller Momente um die x-Achse = 0
5. Summe aller Momente um die y-Achse = 0
6. Summe aller Momente um die z-Achse = 0

Grad der statischen Unbestimmtheit

Um die statische Bestimmtheit eines Systems aus starren Körpern, die über Verbindungselemente miteinander verbunden sind, zu prüfen, kann eine notwendige Bedingung ausgewertet werden.

Hierzu sind die Wertigkeiten sämtlicher Verbindungselemente und der Auflager zu bestimmen und folgende Formel auszuwerten:

n = j+s-3k

Hierbei ist:

j: Summe aller Wertigkeiten der Lager

s: Summe aller Wertigkeiten der Verbindungen

k: Anzahl der freizuschneidenden starren Körper.

Jede Wertigkeit entspricht einer zu bestimmenden Größe (Kräfte oder Momente), während an jedem Körper die oben genannten drei Gleichgewichtsbedingungen (ebener Fall) formuliert werden können.

• für n<0 gilt: in jedem Fall statisch unterbestimmt (instabil, labil)
• für n=0 gilt: notwendig für statische Bestimmtheit
• für n>0 gilt: in jedem Fall statisch unbestimmt, n ist der Grad der statischen Unbestimmtheit

Für ebene Fachwerke, das sind gelenkig verbundene Stäbe, die nur Zug oder Druckkräfte übertragen gilt:

n = a+s-2z

Hierbei ist

a: Anzahl der Auflagerreaktionen

s: Anzahl der Stäbe

z: Anzahl der Gelenke

In jedem Knoten können nur zwei Gleichgewichtsbedingungen formuliert werden, da keine Momente auftreten. Diese Gleichung stellt somit einen Spezialfall der obigen allgemeineren Formel dar. Während die erste Formel auf dem Freischneiden der einzelnen Körper beruht, beruht die zweite Formel auf der Auswertung der Gleichgewichtsbedingungen in jedem Gelenk und entspricht damit in der Herangehensweise dem Knotenpunktverfahren.

Um räumliche Systeme zu erfassen, lassen sich analoge Beziehungen formulieren.

Zusätzliche Schnittgrößen

Verformungen durch Verschiebungen und Verdrehungen der Lager, Temperaturdehnungen, Kriechen und Schwinden des Betons verursachen in statisch bestimmten Systemen keine zusätzlichen Schnittgrößen. In statisch unbestimmten Systemen allerdings entstehen normalerweise immer zusätzliche Schnittgrößen und Spannungen. Um diese Systeme berechnen zu können, muss man Formänderungen und Steifigkeiten der Stäbe mit in die Betrachtungen einbeziehen.

Innere und äußere statische Bestimmtheit

Bei einer Reihe von Stabtragwerken ist es zweckmäßig und anschaulich, zwischen äußerer und innerer statischer Bestimmtheit zu unterscheiden. Ein System oder Systemteil heißt äußerlich statisch bestimmt, falls die äußeren Lagerreaktionen allein mit den Gleichgewichtsbedingungen aus der Belastung berechnet werden können. Ein System heißt innerlich statisch bestimmt, falls die Schnittgrößen (Reaktionen) an geschnittenen Teilsystemen mit Hilfe der Gleichgewichtsbedingungen aus der Belastung berechnet werden können.

Beispiele

Einfache statisch bestimmte Systeme sind:

• Einfeldträger (Träger auf zwei Stützen)
• Träger auf zwei Stützen mit überkragendem Ende
• Kragträger
• Dreigelenkrahmen
• Dreigelenkbogen
• Gerberträger

Einfache statisch unbestimmte Systeme sind:

• Durchlaufträger

(je nach Anzahl der überspannten Felder und der Auflagerbedienungen kann ein Durchlaufträger auch mehrfach statisch unbestimmt sein!)

Beispiele für ein äußerlich bestimmtes, innerlich aber unbestimmtes System:

• Rahmenfachwerkträger
• Vierendeelträger

Siehe auch

• Balkentheorie
• Lager (Statik)
• Stab (Statik)
• Statik (Physik)
• Statische Berechnung
• Dreibein