Faktoralgebra

In der Mathematik versteht man unter einer Kongruenzrelation eine Äquivalenzrelation auf einer algebraischen Struktur, die mit den Operationen dieser algebraischen Struktur verträglich ist. Formal ausgedrückt heißt dies

Definition

Sei A eine Menge, θ eine Äquivalenzrelation auf A und 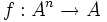$f: A^n \rightarrow A$ sei eine n-stellige Operation (Funktion) auf A. Man nennt θ und f verträglich, falls für alle 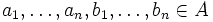$a_1, \dots, a_n, b_1, \dots, b_n \in A$ mit $a_1 \theta b_1, \dots, a_n \theta b_n$ immer

$f(a_1, \dots, a_n) \theta f(b_1, \dots, b_n)$

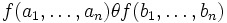
gilt.

Sei nun 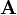$\mathbf{A}$ eine algebraische Struktur mit Grundmenge A und Operationenmenge F. θ wird Kongruenzrelation auf 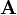$\mathbf{A}$ genannt, falls θ mit allen 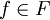$f \in F$ verträglich ist.

Anwendung

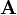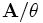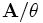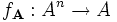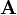Aus einer algebraischen Struktur $\mathbf{A}$ und einer Kongruenzrelation θ auf dieser algebraischen Struktur kann eine neue algebraische Struktur $\mathbf{A} / \theta$ gewonnen werden, die sogenannte Faktoralgebra, dabei ist die Grundmenge von $\mathbf{A} / \theta$ gerade die Faktormenge A / θ und die für jede n-stellige Operation $f_{\mathbf{A}}: A^n \rightarrow A$ von $\mathbf{A}$ wird eine neue Operation 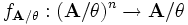$f_{\mathbf{A} / \theta}: (\mathbf{A} / \theta)^n \rightarrow \mathbf{A} / \theta$ auf $\mathbf{A} / \theta$ 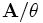definiert durch

$f_{\mathbf{A} / \theta}([a_1]_\theta, \dots, [a_n]_\theta):=[f_{\mathbf{A}}(a_1, \dots, a_n)]_\theta$

Beispiele

1. Für alle algebraischen Strukturen sind 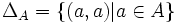$\Delta_A = \{ (a, a) | a \in A \}$ (genannt Diagonale oder Identität) und 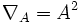$\nabla_A = A^2$ (genannt Allrelation) immer Kongruenzrelationen.
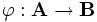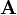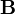2. Ist $\varphi : \mathbf{A} \rightarrow \mathbf{B}$ ein Homomorphismus zwischen den beiden algebraischen Strukturen $\mathbf{A}$ und $\mathbf{B}$. Definiere 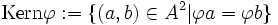$\mbox{Kern} \varphi := \{(a,b) \in A^2 | \varphi a = \varphi b \}$. Dann ist 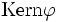$\mbox{Kern} \varphi$ eine Kongruenzrelation auf A.
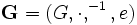3. Sei $\mathbf{G} = (G, \cdot, ^{-1}, e)$ eine Gruppe, N ein Normalteiler dieser Gruppe. θ_N sei diejenige Äquivalenzrelation auf G mit den Äquivalenzklassen 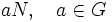$aN, \quad a \in G$, dann ist θ_N eine Kongruenzrelation auf 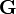$\mathbf{G}$. Man kann sogar zeigen, dass 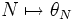$N \mapsto \theta_N$ eine bijektive Abbildung zwischen den Normalteilern und den Kongruenzrelationen einer Gruppe ist. Bei einer Gruppe entsprechen also Kongruenzrelationen genau den Normalteilern.
4. Die analoge Aussage wie oben gilt auch für Ideale von Ringen und für Unterräume von Vektorräumen. (Sprich: Die von Idealen bzw. Unterräumen bestimmten Äquivalenzklassen entsprechen genau den von Kongruenzrelationen bestimmten Klassen).
5. Infolge dessen gibt es für Algebren und Kongruenzen auch einen Homomorphiesatz sowie die beiden Isomorphiesätze. Sie stellen eine Verallgemeinerung der von Gruppen (und Ringen bzw. Vektorräumen) bekannten Sätze dar, sodass der Homomorphiesatz bei den Gruppen in größerem Kontext gesehen werden kann.

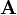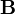Homomorphiesatz (für Algebren): Sind $\mathbf{A}$ und $\mathbf{B}$ zwei Algebren gleichen Typs (d.h. gibt es zu jeder n-stelligen Funktion 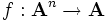$f:\mathbf{A}^n\to\mathbf{A}$ genau eine "passende" n-stelligen Funktion 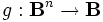$g:\mathbf{B}^n\to\mathbf{B}$) und ist 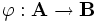$\varphi:\mathbf{A}\to\mathbf{B}$ ein Algebrenhomomorphismus mit Kern 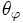$\theta_\varphi$, so gilt: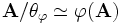 $\mathbf{A} / \theta_\varphi\simeq\varphi(\mathbf{A})$

Ebenso könnte man die Isomorphiesätze formulieren, für die man zuerst geeignet den Begriff der Faktorkongruenz benötigt.