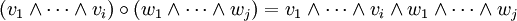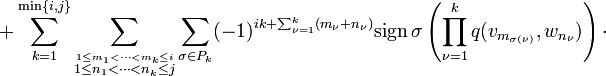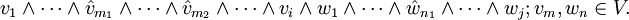- Dachprodukt
-
Die Graßmann-Algebra oder äußere Algebra eines Vektorraums V ist eine assoziative, graduierte Algebra mit Einselement. Sie ist – je nach Definition – eine Unteralgebra oder eine Faktoralgebra der Tensoralgebra und wird durch ΛV dargestellt. Die Multiplikation wird als äußeres Produkt, Keilprodukt oder Wedgeprodukt bezeichnet. Ein Spezialfall dieses Produkts ist mit dem Kreuzprodukt verwandt. Anwendung findet dieser Kalkül in der algebraischen Geometrie und der Differentialgeometrie als Algebra der Differentialformen. In dieser Form geht die Theorie der alternierenden Differentialformen auf Élie Cartan zurück, der damit die bestehenden Begriffe der Flächentheorie vereinheitlichte. Antikommutative Produkte von Vektoren wie auch abstrakte Vektorräume überhaupt wurden erstmals 1846 von Hermann Graßmann betrachtet.
Inhaltsverzeichnis
Formale Definition
Äußere Potenz
Es sei V ein Vektorraum über einem Körper K. Weiter sei
(mit den Konventionen T0(V) = K und T1(V) = V). Der Unterraum
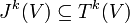 sei erzeugt durch Elementartensoren, bei denen zwei Faktoren gleich sind:
sei erzeugt durch Elementartensoren, bei denen zwei Faktoren gleich sind:Die äußere Potenz ist dann definiert als der Quotientenraum
- Λk(V) = Tk(V) / Jk(V).
Äußere Algebra
Die direkte Summe
ist ein zweiseitiges, homogenes Ideal in der Tensoralgebra
Die äußere Algebra ist die Faktoralgebra
- Λ(V): = T(V) / J(V).
Als Vektorraum aufgefasst ist dies isomorph zu
(Für k > dimV ist Λk(V) = 0, siehe unten.) Das Produkt in der äußeren Algebra wird traditionell als
 geschrieben.
geschrieben.Analog kann man die äußere Algebra von Moduln über kommutativen Ringen definieren.
Alternierende Tensoren
Im folgenden sei die Charakteristik von K gleich 0.
Auf den homogenen Bestandteilen Tk(V) operiert jeweils die symmetrische Gruppe Sk. Ein Tensor
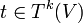 heißt alternierend, wenn
heißt alternierend, wennfür alle Permutationen
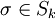 gilt (sgn(σ) ist das Vorzeichen der Permutation). Der Vektorraum der alternierenden Tensoren der Stufe k sei
gilt (sgn(σ) ist das Vorzeichen der Permutation). Der Vektorraum der alternierenden Tensoren der Stufe k sei 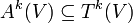 .
.Man kann jedem Tensor mit Hilfe der Antisymmetrisierungsabbildung (auch „Alternator“)
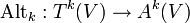 auf kanonische Weise einen alternierenden Tensor zuordnen. Sie ist definiert durch
auf kanonische Weise einen alternierenden Tensor zuordnen. Sie ist definiert durchMit dem Produkt
für
 und bilinearer Fortsetzung wird der Raum
und bilinearer Fortsetzung wird der Raum 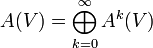 der alternierenden Tensoren zu einer assoziativen, graduiert-kommutativen Algebra. Die kanonische Abbildung
der alternierenden Tensoren zu einer assoziativen, graduiert-kommutativen Algebra. Die kanonische Abbildung 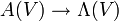 ist ein Algebren-Isomorphismus. Man könnte die äußere Algebra in Charakteristik 0 also auch als die Algebra der alternierenden Tensoren definieren.
ist ein Algebren-Isomorphismus. Man könnte die äußere Algebra in Charakteristik 0 also auch als die Algebra der alternierenden Tensoren definieren.Eigenschaften
- Die Multiplikation ist graduiert-kommutativ, d.h.
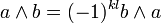 für
für 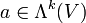 und
und 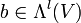 . Insbesondere ist
. Insbesondere ist  für alle
für alle 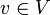 , aber im Allgemeinen ist
, aber im Allgemeinen ist  für
für 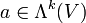 mit k gerade.
mit k gerade. - Es sei
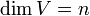 und
und 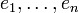 eine Basis von V. Dann ist
eine Basis von V. Dann ist
-
- eine Basis von Λk(V). Die Dimension ist
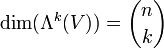 . Insbesondere ist Λk(V) = 0, falls k > n. Die Basis der äußeren Algebra erhält man dann eben durch Vereinigung der Basen aller Grade. Für die Dimension gilt dann
. Insbesondere ist Λk(V) = 0, falls k > n. Die Basis der äußeren Algebra erhält man dann eben durch Vereinigung der Basen aller Grade. Für die Dimension gilt dann
- Es folgt, dass sich jedes Element der Graßmann-Algebra darstellen lässt als
- wobei die 2n Koeffizienten fI das Element bezüglich einer Basis
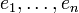 charakterisieren und
charakterisieren und 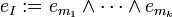 mit
mit 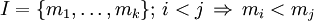 ist.
ist.
- Sind V,W zwei Vektorräume (bzw. Moduln), so entsprechen Homomorphismen
-
- den alternierenden k-multilinearen Abbildungen
- Ist V ein Vektorraum (bzw. Modul) und A eine assoziative Algebra, so gibt es eine Bijektion zwischen
-
- den Homomorphismen von Vektorräumen (bzw. Moduln)
 , so dass f(v)2 = 0 für alle
, so dass f(v)2 = 0 für alle 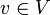 gilt
gilt
- den Homomorphismen von Vektorräumen (bzw. Moduln)
- und
- den Algebrenhomomorphismen
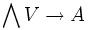 .
.
- den Algebrenhomomorphismen
Graduierung
Die äußere Algebra ΛV kann in Form einer direkten Summe in Bestandteile verschiedenen Grades zerlegt werden. Der Teilvektorraum ΛmV zum Grad m wird dabei von allen äußeren Produkten mit m Faktoren aus (der Einbettung von) V erzeugt. Hat V die Dimension n, so gilt
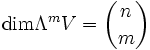 und
und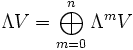 .
.- Die Gesamtdimension der Algebra ist 2n.
In der Physik heißen die Elemente von
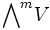 m-Vektoren. 0-Vektoren sind Skalare, d.h. Elemente des Grundkörpers, 2-Vektoren werden häufig Bivektoren genannt, n-Vektoren werden auch als Pseudoskalare bezeichnet.
m-Vektoren. 0-Vektoren sind Skalare, d.h. Elemente des Grundkörpers, 2-Vektoren werden häufig Bivektoren genannt, n-Vektoren werden auch als Pseudoskalare bezeichnet.Beispiel
Man wähle zum Vektorraum
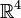 die kanonische Basis. Der 3. Grad der äußeren Algebra
die kanonische Basis. Der 3. Grad der äußeren Algebra 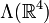 wird aufgespannt durch:
wird aufgespannt durch:Wie man durch Abzählen sofort sieht, ist
 .
.Skalarprodukt
Hat der Vektorraum V ein Skalarprodukt, so kann auch die äußere Algebra mit einem solchen ausgestattet werden. Dabei werden Unterräume verschiedenen Grades als orthogonal definiert. Innerhalb eines Unterraums genügt es, das Skalarprodukt auf reinen Produkten zu definieren, seien
 und
und  reine Produkte in ΛmV. Ihnen kann die Gramsche Matrix der Skalarprodukte zugeordnet werden. Dann kann das Skalarprodukt als Determinante der Gramschen Matrix definiert werden:
reine Produkte in ΛmV. Ihnen kann die Gramsche Matrix der Skalarprodukte zugeordnet werden. Dann kann das Skalarprodukt als Determinante der Gramschen Matrix definiert werden:Ist V der n-dimensionale Spaltenvektorraum, so kann zu
 die Matrix
die Matrix 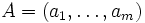 definiert werden. Von dieser kann man die maximalen quadratischen Untermatrizen Aα betrachten. Dabei ist α ein Multiindex aus
definiert werden. Von dieser kann man die maximalen quadratischen Untermatrizen Aα betrachten. Dabei ist α ein Multiindex ausund Aα besteht aus genau diesen Zeilen von A.
Es gilt folgende Identität, im Falle m=2 und A=B auch "Flächenpythagoras" genannt:
Differentialformen
Das Hauptanwendungsgebiet der äußeren Algebra liegt in der Differentialgeometrie. Sei M eine n-dimensionale differenzierbare Mannigfaltigkeit. So wählt man den Kotangentialraum dieser Mannigfaltigkeit als zugrundeliegenden Vektorraum und bildet die äußere Algebra. Dieser neue Vektorraum ist der Raum der Differentialformen. Diese Formen haben den großen Vorteil, dass man mit ihrer Hilfe Karten-unabhängig auf einer Mannigfaltigkeit integrieren kann.
Hodge-Operator
Sei V (wie oben) ein Vektorraum und ΛnV die äußere Algebra von V. Sei
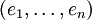 eine orientierte Basis von V. Der Hodge-Operator oder Hodge-Stern-Operator ist ein natürlicher Isomorphismus
eine orientierte Basis von V. Der Hodge-Operator oder Hodge-Stern-Operator ist ein natürlicher Isomorphismus 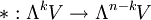 mit
mit 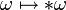 . Der Hodge-Operator ordnet also jedem
. Der Hodge-Operator ordnet also jedem 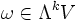 auf eindeutige Weise ein
auf eindeutige Weise ein 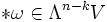 zu. Für dieses gilt
zu. Für dieses giltBeziehung zum Kreuzprodukt
Wir wählen die kanonische Basis e1,e2,e3 des
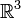 . Weiter wählen wir zwei Elemente α = a1e1 + a2e2 + a3e3 und
. Weiter wählen wir zwei Elemente α = a1e1 + a2e2 + a3e3 und 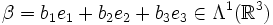 aus der äußeren Algebra (bzw. äußeren Potenz) des reellen Vektorraumes.
aus der äußeren Algebra (bzw. äußeren Potenz) des reellen Vektorraumes.* bezeichne den Hodge-Operator. Für das äußere Produkt von α,β gilt mithilfe des Distributivgesetzes
Der Hodge-Operator ordnet im dreidimensionalen Raum dem Produkt der Basisvektoren
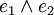 den Vektor e3 zu. Durch zyklisches Vertauschen der Indizes ergeben sich die Zuordnungen der anderen Basisvektoren. Damit ergibt sich das Kreuzprodukt im dreidimensionalen reellen Raum. Also kann man
den Vektor e3 zu. Durch zyklisches Vertauschen der Indizes ergeben sich die Zuordnungen der anderen Basisvektoren. Damit ergibt sich das Kreuzprodukt im dreidimensionalen reellen Raum. Also kann man 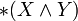 auf der äußeren Algebra als Verallgemeinerung des Kreuzproduktes verstehen. Mit Hilfe dieser Verallgemeinerung lässt sich ebenfalls die aus der Vektoranalysis bekannte Funktion rot (Rotation) auf den n-dimensionalen Fall verallgemeinern.
auf der äußeren Algebra als Verallgemeinerung des Kreuzproduktes verstehen. Mit Hilfe dieser Verallgemeinerung lässt sich ebenfalls die aus der Vektoranalysis bekannte Funktion rot (Rotation) auf den n-dimensionalen Fall verallgemeinern.Beziehung zur Clifford-Algebra
Sei
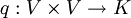 eine symmetrische Bilinearform auf V. Nun sei die zweistellige, bilineare Verknüpfung
eine symmetrische Bilinearform auf V. Nun sei die zweistellige, bilineare Verknüpfung 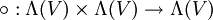 definiert durch:
definiert durch:Die Hüte über den Faktoren bedeuten hier deren Auslassung im Produkt. Durch Einführen dieser neuen Verknüpfung als Multiplikation erhält man die Clifford-Algebra Cl(V,q). Insbesondere erhält man mit der Nullbilinearform wieder die Graßmann-Algebra: Cl(V,0) = Λ(V), da der Zusatzterm in der obigen Gleichung wegfällt und somit
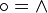 gilt.
gilt.Literatur
- Kowalsky, H.J. und Michler, G.: Lineare Algebra
- Abraham, R., Marsden, J.E. and Ratiu T.: Manifolds, Tensor Analysis, and Applications
Weblinks
Wikimedia Foundation.

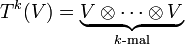
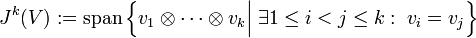
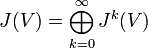
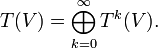
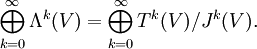
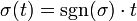
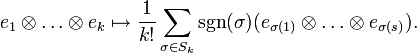
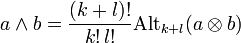
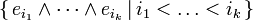
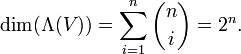
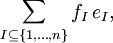
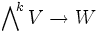
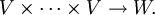

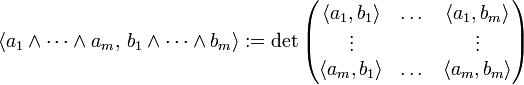

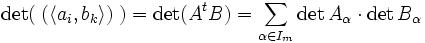

![\begin{array}{rl}
*(\alpha \wedge \beta)
=& *((a_1 e_1 + a_2 e_2 + a_3 e_3) \wedge (b_1 e_1 + b_2 e_2 + b_3 e_3))\\[0.5em]
=& *((a_2e_2\wedge b_1e_1) + (a_3e_3 \wedge b_1e_1) + (a_1e_1 \wedge b_2e_2) \\
&+ (a_3e_3 \wedge b_2 e_2) + (a_1e_1 \wedge b_3e_3) + (a_2b_2 \wedge b_3e_3))\\[0.5em]
=& *((a_1b_2-a_2b_1)(e_1\wedge e_2) + (a_2b_3-a_3b_2) (e_2\wedge e_3) + (a_3b_1-a_1b_3) (e_3\wedge e_1))
\end{array}](/pictures/dewiki/102/fb7cab9930e2bf4d51af9f46a7a325af.png)