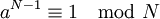Fermat'scher Primzahltest

Mit dem fermatschen Primzahltest kann man Primzahlen von zusammengesetzten Zahlen unterscheiden. Der Test erhält eine Zahl n und eine Basis a als Eingabe. n muss eine ungerade Zahl > 3 sein. Außerdem muss a die Bedingung 1 < a < n − 1 erfüllen. Der Test liefert eines von zwei möglichen Ergebnissen: entweder

• „n ist (bezüglich a) Primzahlkandidat (engl: probable prime)“ oder
• „n ist keine Primzahl“.

Im letzteren Fall ist n keine Primzahl. Falls der Test n zum Primzahlkandidaten erklärt, kann man in den meisten Fällen davon ausgehen, dass n eine Primzahl ist. n ist also "wahrscheinlich" eine Primzahl. Daher wird dieses Verfahren auch PRP-Test (= probable prime test) genannt.

Fermatscher Primzahltest

Der fermatsche Primzahltest besteht aus zwei Teilen:

• $a^{N-1}\equiv 1 \mod N$

Das ist der kleine fermatsche Satz. Dieser Satz alleine reicht noch nicht aus, um als zuverlässiger Primzahltest zu funktionieren. Deshalb ist noch eine zweite Bedingung notwendig:

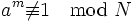• $a^m\not\equiv 1 \mod N$ für alle $m = 1, 2, \ldots , N-2$

für N > 1 und a > 1, wobei N die zu prüfende Zahl ist.

Wie der fermatsche Test arbeitet

Der fermatsche Primzahltest besteht aus zwei Schritten:

1. Berechne $b = a^{n-1} \mod n$.
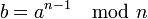2. Falls b = 1, gib "n ist (bezüglich a) Primzahlkandidat" aus, andernfalls "n ist keine Primzahl".

Dabei bedeutet die Operation 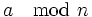$a \mod n$ den Divisionsrest der ganzzahligen Division von a durch n (siehe auch Kongruenz in der Zahlentheorie). Jedoch sollte man beachten, dass die Basis a - selbst wenn diese prim ist - vom Test nicht als Primzahl erkannt wird, da $n^m \equiv 0 \mod n$ für alle n und m gilt.

Korrektheit des fermatschen Primzahltests

Direkt aus dem kleinen fermatschen Satz folgt:

Wenn p eine Primzahl ist, dann gilt für jede Zahl a, die teilerfremd zu p ist: $a^{p-1} \equiv 1 \mod p$

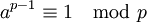
Falls n und a die ursprünglichen Bedingungen erfüllen, dann ist a nicht durch n teilbar. Falls n eine Primzahl ist, so ist aufgrund des kleinen fermatschen Satzes b = 1. Ist b nicht gleich 1, dann ist n keine Primzahl, und der Test gibt „n ist keine Primzahl“ aus.

Ist p eine Primzahl, dann ist n^{p − 1} − 1 durch p teilbar für alle natürlichen Zahlen n < p.

Dies kann man mit Hilfe der Modulo-Funktion schreiben als:

Für alle Primzahlen p gilt 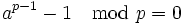$a^{p-1} - 1 \mod p = 0$ mit $2 \le a &amp;lt; p$.

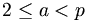oder auch:

Für alle Primzahlen p gilt 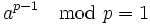$a^{p-1} \mod p = 1$ mit $2 \le a &amp;lt; p$.

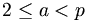Beispiel: p = 5 ist eine Primzahl

a=2	25 − 1 − 1 = 15	wobei	15	durch 5 teilbar ist
a=3	35 − 1 − 1 = 80	wobei	80	durch 5 teilbar ist
a=4	45 − 1 − 1 = 255	wobei	255	durch 5 teilbar ist

Wie man den fermatschen Primzahltest benutzt

Den fermatschen Primzahltest setzt man ein, wenn man eine (große) Zahl n gegeben hat, von der man herausfinden möchte, ob sie eine Primzahl ist oder nicht. In den meisten Fällen reicht es dann nämlich, den fermatschen Primzahltest mit a = 2 zu starten, um die richtige Antwort zu finden:

n        3   4   5   6   7   8   9   10   11   12   13   14   15   16
2^(n-1)  1   0   1   2   1   0   4    2    1    8    1    2    4    0
(mod n)

n        17   18   19    20   21   22   23   24   25   26   27   28   29
2^(n-1)   1   14    1     8    4    2    1    8   16    2   13    8    1
(mod n)

Diese Tabelle könnte man noch bis über 300 fortsetzen und immer würde nicht nur unter jeder Primzahl eine 1 stehen (das muss sowieso der Fall sein, wegen des kleinen fermatschen Satzes), sondern und auch unter jeder zusammengesetzten Zahl eine Zahl verschieden von 1 -- das ist durch den kleinen fermatschen Satz nicht garantiert. Erst mit 341 ist das erste Mal ein Primzahlkandidat bezüglich 2 keine Primzahl, sondern eine zusammengesetzte Zahl, nämlich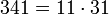 $341=11\cdot 31$. Eine Zahl, die zwar ein Primzahlkandidat, aber keine Primzahl ist, wird Pseudoprimzahl genannt. Bis 2000 gibt es 303 Primzahlen, aber nur 7 Pseudoprimzahlen bezüglich 2, nämlich 341, 561, 645, 1105, 1387, 1729 und 1905.

Wählt man nicht a = 2, sondern eine andere erlaubte Zahl, so kommt man zu ähnlichen Ergebnissen. Dies muss auch so sein, denn Paul Erdős hat bewiesen, dass die Pseudoprimzahlen zu einer festen Basis a verschwindend wenige sind im Vergleich zu den Primzahlen.

Gegenbeispiel: p = 55 ist keine Primzahl, denn für n = 2 gilt:

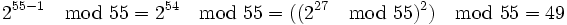$2^{55-1} \mod 55 = 2^{54} \mod 55 = ((2^{27} \mod 55)^2) \mod 55 = 49$ ungleich 1

Das bedeutet, dass die Zahl p = 55 keine Primzahl ist.

Annahme, für eine natürliche Zahl n > 1 gelte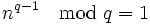

$n^{q-1} \mod q = 1$. Wenn jetzt zutreffen würde, dass q dann auch eine Primzahl ist, dann hätte man ein gutes Verfahren zum Testen auf Primzahlen. Dass dem nicht so ist, daran sind die Pseudoprimzahlen schuld.

Pseudoprimzahlen

Es gibt Zahlen q, die keine Primzahlen sind und für die dennoch gilt:

nq − 1 − 1 durch q teilbar für bestimmte natürlichen Zahlen n < q, bei denen n kein Teiler von q ist.

Solche Zahlen heißen Pseudoprimzahlen.

Beispiel: q = 21 ist eine Pseudoprimzahl, da für n = 13 gilt

$13^{21-1} \mod 21 = 13^{20} \mod 21 = ((13^{10} \mod 21)^2) \mod 21 = 1$

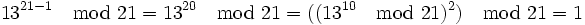
obwohl 21 eine zusammengesetzte Zahl der Form 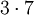$3\cdot 7$ ist.

Carmichael-Zahlen

Besonders hartnäckige Pseudoprimzahlen sind die Carmichael-Zahlen, für die gilt, dass alle Basen n mit 1 < n < q, die nicht Teiler von q sind:

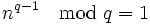$n^{q-1} \mod q = 1$ (für alle n teilerfremd zu q)

Als Beispiel dafür die 561 (sie ist die kleinste Carmichael-Zahl):

Basis 3: $3^{560} \mod 561 = ((2^{280} \mod 561)^2)\mod 561 = 375$

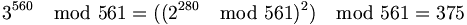
Basis 11: $11^{560} \mod 561 = ((2^{280} \mod 561)^2)\mod 561 = 154$

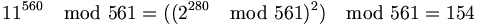
Auch für die Basen n = 17,33,51 und 187, die alle Teiler von 561 sind, gilt, dass n⁵⁶⁰ modulo 561 ungleich 1 ist. Für alle anderen Basen n, die keine Teiler von 561 sind, gilt

$n^{560} \mod 561 = ((a^{280} \mod 561)^2) \mod 561 = 1$.

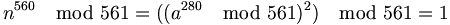Was kann man tun, wenn man 100%-sichere Ergebnisse bekommen will

Wenn man nur auf die Basis 2 testet, dann kann man nur bis 340 sicher sein, dass man ein korrektes Ergebnis bekommt. Wenn man parallel auf mehrere Basen (zum Beispiel 2, 3 und 5) testet, erhöht sich die sichere Grenze nach oben:

Bei einem Test zur Basis 2 und 3 ist 1105 die erste Pseudoprimzahl, bei 2, 3 und 5 ist 1729 erste Pseudoprimzahl, bei 2, 3, 5, 7 und 11 liegt die sichere Grenze bei 29340 und bei 2, 3, 5, 7, 11 und 13 liegt sie bei 162401. Leider macht jede weitere Basis ein Programm langsamer. Wenn man konsequent auf alle Basen testet, bekommt man zwar ein Programm, das zu 100% sichere Primzahlen zurückliefert, aber viel langsamer als ein Programm ist, das eine Zahl konsequent auf alle möglichen Teiler testet.

Quellcode

Hier ein Programm dazu: C-Quellcode für ein Programm, das nach dem kleinen fermatschen Satz, Primzahlen, Pseudoprimzahlen und Carmichaelzahlen unterscheidet:

 /* Ein Programm, zur Ermittlung von Primzahlen, Pseudoprimzahlen */
 /* und Charmichaelzahlen (starke Pseudoprimzahlen) */
 /* Ein extrem langsames Programm */
 
 #include <stdio.h>
 
 int primfeld[400000];
 int tst[400000];
 
 unsigned long modup(unsigned long x, unsigned long y)
 {
   unsigned long mindex, xtemp = 1;
   for(mindex=1;mindex<=(y-1);mindex++)
   {
     xtemp *= x;
     xtemp %=y;
   }
   return(xtemp);
 } 
 
 void main()
 {
   unsigned long index, index2, anzp=1, m, dtm;
   int tm1, tm2, tm3, gtm;
   FILE *prim;
   FILE *pspr;
   FILE *cnbr;
   prim = fopen("prim.dat","w");
   pspr = fopen("pspr.dat","w");
   cnbr = fopen("cnbr.dat","w");
   primfeld[1] = 2;
   for(index=3;index<=4000000;index++)
   {
     tm1 = 0;
     tm2 = 0;
     tm3 = 0;
     /* faktor$ = "" */
     for(index2=1;index2<=anzp;index2++)
     {
       m = modup(primfeld[index2], index);
       tst[index2] = m;
       if (m == 1)
       {
         tm1 = 1;
         tm3++;
       }
       if ( m != 1) { tm2 = 2; }
     }
     gtm = tm1 + tm2;
     if (gtm == 1)
     {
       anzp++;
       primfeld[anzp] = index;
       fprintf(prim,"%d \n",index);
     }
     if (gtm == 3)
     {
       dtm=anzp/2;
       if (tm3 < dtm)
       {
         fprintf(pspr,"%d: ",index);
         for(index2=1;index2<=anzp;index2++)
         {
           m = modup(primfeld[index2], index);
           if (m == 1)
           {
             fprintf(pspr,"%d, ",primfeld[index2]);
           }
         }
         fprintf(pspr,"\n",0);
       }
       if (tm3 >= dtm)
       {
         fprintf(pspr,"%d: ",index);
         for(index2=1;index2<=anzp;index2++)
         {
           m = modup(primfeld[index2], index);
           if (m != 1)
           {
             fprintf(cnbr,"N%d, ",primfeld[index2]);
           }
         }
         fprintf(cnbr,"\n",0);
       }
     }
   }
   fclose(prim);
   fclose(pspr);
   fclose(cnbr);
 }

Obwohl das Programm zu 100 % korrekte Primzahlen zurückliefert, ist es weniger als Primzahltest, sondern vielmehr als Sieb für Pseudoprimzahlen und Carmichael-Zahlen geeignet.

Der Weg zum probabilistischen Primzahltest

Man kann nun versuchen, diesen Test zu vereinfachen und den Rechenaufwand deutlich zu reduzieren, wenn man eine etwas geringere Wahrscheinlichkeit in der Primzahlaussage in Kauf nimmt.

Dabei gibt es zwei Aspekte:

Suche mit nur einer Basis, bei zufälliger Auswahl der zu testenden Zahl

Wenn man nur eine Basis nimmt, vorzugsweise die Basis 2, dann hat man eine relativ geringe Wahrscheinlichkeit, aber den Umstand, dass wenn man schon eine Pseudoprimzahl wie 341 trifft, dass diese zu 100% falsch ist, auch wenn die Wahrscheinlichkeit auf die 341 zu treffen nur gering ist. Jedesmal, wenn man auf 341 prüft, wird der kleine fermatsche Satz in der Kombination mit 341 und Basis 2 das Urteil „Primzahl“ zurückgeben.

Breitensuche mit zufälliger Auswahl einer oder mehrerer Basen (mit möglicher zufälliger Auswahl der zu testenden Zahl)

Der andere Aspekt ist die Prüfung in der Breite. Bezogen auf die 68 möglichen Primzahlbasen liefern 21 Primbasen für die 341 falsch das Ergebnis "Primzahl" zurück. Das ist ein bisschen weniger als 1/3.

Hier würde eine Verwendung der eulerschen Formel anstelle des kleinen Fermat zu einer Verringerung der Anzahl der ein falsches Ergebnis liefernden Primbasen führen. Wo beim kleinen Fermat zur Pseudoprimzahl 91 noch 8 Primbasen (3, 17, 23, 29, 43, 53, 61 und 79) falsch eine Primzahl melden, sind es bei der eulerschen Formel noch die Hälfte (17, 29, 53 und 79). Das verbessert einen probabilistischen Ansatz erheblich.

Im Fall der Carmichael-Zahl 561 lügen 99 von 102 Primzahlbasen. Bei größeren Carmichaelzahlen, die oft aus nicht viel mehr Primfaktoren zusammengesetzt sind, wird das Missverhältnis noch extremer. Darum vermeiden bessere probabilistische Primzahltests das Problem der Carmichael-Zahlen.

Hier eine Tabelle von besonders guten Pseudoprimzahlen (die keine Carmichael-Zahlen sind). Die 15 ist aufgeführt, weil sie die erste Pseudoprimzahl ist, und die 91 ist in ihrer Umgebung eine relativ gute Pseudoprimzahl.

Pseudoprimzahl	A	B	C	Primfaktoren
15	6	1	83,33%	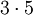$3 \cdot 5$
91	24	8	66,67%	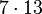$7 \cdot 13$
703	126	56	55,56%	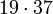$19 \cdot 37$
1891	290	139	52,07%	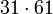$31 \cdot 61$
2701	393	191	51,4%	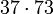$37 \cdot 73$
11305	1366	667	50,44%	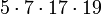$5 \cdot 7 \cdot 17 \cdot 19$
12403	1480	739	50,07%	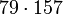$79 \cdot 157$
13981	1650	815	50,06%	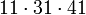$11 \cdot 31 \cdot 41$
18721	2137	1070	49,93%	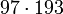$97 \cdot 193$

A: Anzahl der Primzahlen zwischen 2 und der entsprechenden Pseudoprimzahl

B: Anzahl der Primzahlen aus A, die fälschlicherweise behaupten, die entsprechende Pseudoprimzahl sei eine Primzahl

C: Die Wahrscheinlichkeit, bei Auswahl einer Primzahlbasis eine der nicht lügenden zu bekommen

Bei den Carmichael-Zahlen geht die Wahrscheinlichkeit, eine der nichtlügenden Primzahlbasen zu bekommen, gegen 0.

Wenn man zufällig mehrere Primzahlbasen auswählt, dann steigt die Wahrscheinlichkeit, Pseudoprimzahlen als solche zu entlarven:

Anzahl der testenden Primzahlbasen

	1	2	3	4	5
91	83,33%	89,86%	97,23%	99,34%	99,86%
561	2,94%	5,82%	8,65%	11,42%	14,13%
703	55,56%	80,44%	91,48%	96,33%	98,44%
1729	1,11%	2,22%	3,32%	4,41%	5,49%
1891	52,07%	77,11%	89,11%	94,85%	97,56%

Für die Praxis bedeutet das: Oft reicht der Nachweis aus, dass p pseudoprim ist zur Basis 2. Will man die Sicherheit weiter erhöhen, dann muss man eben weitere Zeugen finden, d. h. weitere Zahlen a, zu deren Basis p pseudoprim ist. Im Grenzfall testet man alle Zahlen a < p, d. h., man führt den gesamten Fermattest durch.

Verbesserungen des fermatschen Primzahltests

• 1891 wurde der fermatsche Primzahltest von Édouard Lucas als Lucas-Test verbessert.

• 1967 wurde dieser Lucas-Test nochmal von Brillhart und Selfridge verbessert.

Primzahltest nach Solovay-Strassen

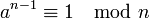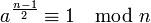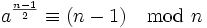Der Solovay-Strassen-Test benutzt nicht den kleinen fermatschen Satz: $a^{n-1} \equiv 1 \mod n$, sondern den etwas strengeren Satz nach Euler: $a^{\frac{n-1}{2}} \equiv 1 \mod n$ bzw. $a^{\frac{n-1}{2}} \equiv (n-1) \mod n$. Außerdem wird das Ergebnis noch mit dem Jacobi-Symbol J(a,n) abgeglichen.

Gary Miller und Michael O. Rabin verbesserten den Fermattest im so genannten Miller-Rabin-Test. Nicht-Primzahlen kann der Solovay-Strassen-Test mit Wahrscheinlichkeit 1/2 pro Durchlauf erkennen (der Miller-Rabin-Test mit seinem geringeren Aufwand sogar mit 3/4). Eine k-malige Wiederholung des Tests verringert die Wahrscheinlichkeit, dass eine Nichtprimzahl den Test besteht, auf 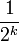$\frac{1}{2^k}$ (bzw. auf 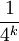$\frac{1}{4^k}$ beim Miller-Rabin-Test, der daher den ersten genannten praktisch vollkommen ersetzt hat). Im Jahre 1980 stellten die Mathematiker Leonard M. Adleman, R.S. Rumely, H. Cohen und H.W. Lenstra Jr den nach ihnen benannten ARCL-Test vor. Dieser ist eine Weiterentwicklung des fermatschen Primzahltests, indem er Carmichael-Zahlen erkennt.

Literatur

• Carl Pomerance, John L. Selfridge, Samuel S. Wagstaff Jr.: The pseudoprimes to 25 · 109, in: Mathematics and Computation 35:151, 1980, S. 1003–1026.
• Paulo Ribenboim: The new Book of Prime Number Records, Springer, New York 1996, ISBN 0-387-94457-5