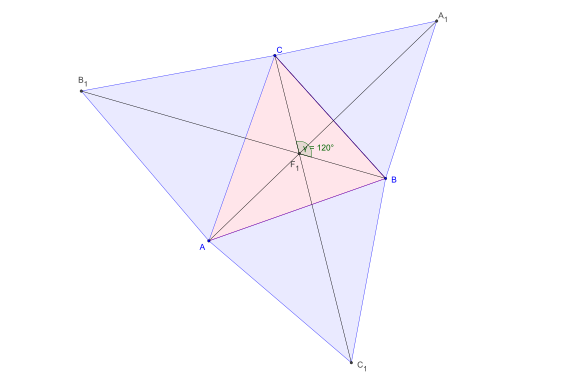
Fermat Punkt

Die beiden Fermat-Punkte, benannt nach dem französischen Rechtsanwalt und Mathematiker Pierre de Fermat, gehören zu den besonderen Punkten eines Dreiecks. Über den Seiten eines gegebenen Dreiecks ABC zeichnet man drei gleichseitige Dreiecke. Verbindet man die neu dazu gekommenen Punkte A1, B1 und C1 mit den gegenüber liegenden Ecken des Dreiecks (also mit A, B bzw. C), so schneiden sich diese Verbindungsstrecken in einem Punkt F. Dieser wird als erster Fermat-Punkt des Dreiecks bezeichnet. Der 1. Fermatpunkt findet in der Wirtschaftsmathematik, speziell in der Standortplanung Anwendung. Angenommen drei Unternehmen wollen ein Zentrallager derart bauen, dass die Transportkosten zu diesem Zentrallager minimal sind. Das Zentrallager müsste an der Stelle des Fermatpunkts gebaut werden, wenn man sich die Lage der drei Unternehmen als Dreieck vorstellt, da für den Fermatpunkt die Summe der Abstände zu den Ecken des Dreiecks minimal ist (wobei alle Winkel im Dreieck kleiner als 120° sein müssen).

Der zweite Fermat-Punkt eines Dreiecks ergibt sich nach der gleichen Konstruktion wie der erste Fermat-Punkt, nur muss man die gleichseitigen Dreiecke jeweils nicht „nach außen“ über den Dreiecksseiten errichten, sondern „nach innen“. Er besitzt im wesentlichen die gleichen Eigenschaften wie der erste Fermatpunkt, allerdings erscheint bei ihm immer eine Seite unter einem Winkel von 120° und zwei Seiten unter einem Winkel von 60°

Eigenschaften

• Wenn alle Winkel des Dreiecks ABC kleiner als 120° sind, dann ist der erste Fermat-Punkt des Dreiecks derjenige Punkt im Inneren des Dreiecks, von dem aus alle drei Seiten unter einem 120°-Winkel erscheinen; dies bedeutet

  $\angle BFC = \angle CFA = \angle AFB = 120^{\circ}$.

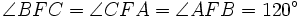• Ist ein Winkel von Dreieck ABC größer oder gleich 120° (beispielsweise 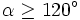$\alpha \geq 120^{\circ}$), dann gilt stattdessen

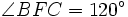  $\angle BFC = 120^{\circ}$ und $\angle CFA = \angle AFB = 60^{\circ}$.

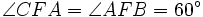Dieser Fall gilt immer für den zweiten Fermatpunkt.

• Sind alle Winkel des gegebenen Dreiecks ABC kleiner als 120°, so ist der erste Fermat-Punkt derjenige Punkt, für den die Summe der Entfernungen von den Ecken des Dreiecks ABC (also die Summe 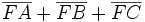$\overline{FA} + \overline{FB} + \overline{FC}$) den kleinstmöglichen Wert annimmt.
  

Der Beweis dieser Tatsache stammt von dem Italiener Evangelista Torricelli. Daher spricht man gelegentlich auch vom Fermat-Torricelli-Punkt. Ist dagegen ein Winkel des Dreiecks ABC größer oder gleich 120°, dann ist nicht mehr der 1. Fermat-Punkt der Punkt mit der kleinstmöglichen Summe der Entfernungen, sondern die Ecke, an der dieser Winkel liegt.

• Die zwei Fermat-Punkte sind isogonal konjugiert zu den beiden isodynamischen Punkten.
• Die Fermat-Punkte liegen auf der Kiepert-Hyperbel.

Koordinaten

Fermat-Punkte (X13 und X14)
Trilineare Koordinaten	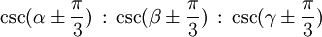$\csc(\alpha\pm\frac{\pi}{3}) \, : \, \csc(\beta\pm\frac{\pi}{3}) \, : \, \csc(\gamma\pm\frac{\pi}{3})$
Baryzentrische Koordinaten	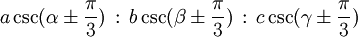$a \csc(\alpha\pm\frac{\pi}{3}) \, : \, b \csc(\beta\pm\frac{\pi}{3}) \, : \, c \csc(\gamma\pm\frac{\pi}{3})$

Siehe auch

Ausgezeichnete Punkte im Dreieck

Weblinks

• Fermat.html - eine Java-Visualisierung mit Hilfe von GeoGebra.