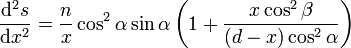- Prinzip von Fermat
-
Das Fermat'sche Prinzip (nach Pierre de Fermat) besagt, dass Licht in einem Medium in der Regel den schnellsten Weg von einem Punkt zum anderen nimmt.
Es verhält sich so wie ein Rettungsschwimmer, der jemanden im Wasser retten will. Um ihm schnellstens zu Hilfe zu kommen, läuft er schnell am Strand auf einen Punkt zu, von dem aus der Weg durch das Wasser kurz ist und daher fast rechtwinklig zum Strand verläuft. Zwar ist dieser Weg länger als der direkte, aber es geht weniger Zeit mit langsamem Schwimmen verloren.
Nach dem Fermat'schen Prinzip sind Lichtstrahlen in jedem homogenen Medium gerade.
An Grenzflächen zweier homogener Medien gilt das Reflexionsgesetz, dass Einfalls- und Ausfallswinkel übereinstimmen, und das Snelliussche Brechungsgesetz, dass Licht zum optisch dichteren Medium gebrochen wird. In einem inhomogenen Medium mit ortsabhängiger Brechzahl durchläuft Licht gekrümmte Bahnen.
Daher erscheint zum Beispiel die untergehende Sonne abgeflacht: die Lichtstrahlen vom oberen Rand der Sonne werden weniger gebrochen als die vom unteren Rand.
Inhaltsverzeichnis
Mathematische Formulierung
Mathematisch gesagt durchläuft Licht in einem Medium mit Brechzahl
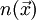 zwischen den Punkten
zwischen den Punkten 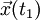 und
und 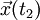 von allen denkbaren Bahnen
von allen denkbaren Bahnen 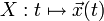 durch diese Punkte diejenige Bahn, auf der die Laufzeit
durch diese Punkte diejenige Bahn, auf der die Laufzeitminimal, genauer stationär, ist. Die Größe τ hat die Bedeutung der Lichtlaufzeit zwischen beiden Punkten, denn die Brechzahl ist an jedem Ort das Verhältnis der Vakuumlichtgeschwindigkeit c zur dortigen Lichtgeschwindigkeit v im Medium,
Meist ist die Lichtlaufzeit ein Minimum, das heißt: Jede kleine Änderung der Bahn vergrößert die Laufzeit. Dies muss aber nicht immer so sein, wie die rechte Abbildung zeigt. Für eine Bahn zwischen den zwei Brennpunkten S und P einer Ellipse sind drei mögliche Fälle eingezeichnet.
- Bei Reflexion an einer Fläche mit einer geringeren Krümmung als jene der Ellipsoidfläche ist die Laufzeit minimal.
- Bei Reflexion an der Ellipsoidfläche sind alle Punkte auf der Fläche gleichwertig: Bei Verschieben des Reflexionspunkts auf der Ellipsoidfläche ändert sich die Laufzeit nicht.
- Bei Reflexion an einer Fläche mit einer größeren Krümmung als jene der Ellipsoidfläche ist die Laufdauer, verglichen mit anderen Reflexionspunkten auf dieser Fläche, maximal. Dies tritt bei Reflexion an einem Hohlspiegel auf.
Beispiel Brechungsgesetz
Um das Fermat'sche Prinzip zu erfüllen, muss die Weglänge s(x) extremal werden
Erfüllt ist
für
Um Maximum und Minimum zu unterscheiden, ist die zweite Ableitung nötig
Diese ist i.A. positiv. Licht wird entlang der durchgezogenen Linie gebrochen, die optische Weglänge ist minimal.
Die Ableitung ist jedoch negativ, wenn | n' | > | n | ( | β | < | α | ) und (d − x) < 0. In diesem Fall ist β < 0, was bei positivem α und n nur für n' < 0 erfüllt ist. Licht wird entlang der gestrichelten Linie gebrochen, die optische Weglänge ist maximal. Negative Brechungsindezes sind spezielle Eigenschaften sog. Metamaterialien
Siehe auch
Literatur
- Scheck: Theoretische Physik 3. Klassische Feldtheorie. ISBN 3540422765. Kapitel 4.4 Geometrische Optik, 4.4.3 Medien mit negativem Brechungsindex
Weblinks
- Roger Erb: Geometrische Optik mit dem Fermat-Prinzip. Aus: Physik in der Schule. 30, Nr. 9, 1992, S. 291-295.
Wikimedia Foundation.

![\tau[X] = \frac{1}{c}\,\int_{t_1}^{t_2} n(\vec{x}(t))\, \sqrt{\left(\frac{\mathrm d \vec{x}(t)}{\mathrm d t}\right)^2}\, \mathrm d t](/pictures/dewiki/101/e097f4ebf8908beaa43e123706fc400f.png)
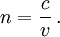


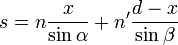
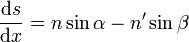
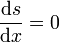
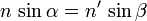 (
(