Fermatsches Prinzip

Das Fermatsche Prinzip (nach Pierre de Fermat) besagt, dass Licht in einem Medium zwischen zwei Punkten Wege nimmt, auf denen seine Laufzeit bei kleinen Variationen des Weges stationär ist, insbesondere (optisch) kürzeste und längste.

Aus dem Fermatschen Prinzip lassen sich das snelliussche Brechungsgesetz und das Reflexionsgesetz herleiten. Außerdem ergibt sich, dass Lichtstrahlen in jedem homogenen Medium gerade verlaufen.

Ein verwandtes Beispiel

Der Rettungsschwimmer wird den grünen Weg nehmen um möglichst schnell zum Ertrinkenden zu kommen.

Die Herleitung des Brechungsgesetzes aus dem Fermatschen Prinzip ist verwandt mit der Frage, welchen Weg ein Rettungsschwimmer nehmen sollte, der jemanden aus dem Wasser retten will. Ziel ist es natürlich, dem Ertrinkenden möglichst schnell zu Hilfe zu kommen. Dazu läuft der Rettungsschwimmer schnell am Strand auf einen Punkt zu, von dem aus der Weg durch das Wasser kurz ist, da er sich dort nur langsam fortbewegen kann. Läuft er aber zu weit, dann wird der Anteil des Weges im Wasser kaum noch kürzer, aber die Strecke an Land deutlich länger. Der im Bild grün eingezeichnete Weg ist der insgesamt schnellste. Der Rettungsschwimmer muss aber nicht lange überlegen, denn wenn er den optimalen Punkt knapp verfehlt, ist die Zeit kaum länger, direkt am optimalen Punkt ändert sich die Zeit bei einer kleinen Variation gar nicht.

Diese Stationarität ist der Kern des Fermatschen Prinzips. Sie findet sich auch in der Umgebung eines (lokal) längsten Weges.

Herleitung des Brechungsgesetzes

Darstellung des Brechungsgesetzes am Beispiel des Übergangs von einem Material zu einem Material höherer Brechzahl

Aus dem Fermatschen Prinzip lässt sich sehr elegant das Brechungsgesetz von Snellius herleiten:

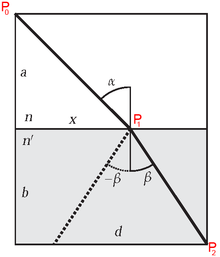
In der Abbildung rechts legt der Lichtstrahl den Weg von links oben P₀ = (0,a + b) über P₁ = (x,b) nach rechts unten P₂ = (d,0) zurück. Im oberen Medium sei die Lichtgeschwindigkeit c₁ und im unteren Teil c₂. Damit ergibt sich für die Laufzeit:

$t(x) = t_1 + t_2 = \frac{s_1}{c_1} + \frac{s_2}{c_2} = \frac{|P_1 - P_0|}{c_1} + \frac{|P_2 - P_1|}{c_2} = \frac{\sqrt{a^2+x^2}}{c_1} + \frac{\sqrt{(d-x)^2+b^2}}{c_2}$

Durch Ableiten nach x finden wir den Extremalwerte von t.

$0 \stackrel{!}{=} \frac{dt}{dx} = \frac{1}{c_1} \frac{1}{2} \frac{1}{\sqrt{a^2+x^2}} 2 x + \frac{1}{c_2} \frac{1}{2} \frac{1}{\sqrt{(d-x)^2+b^2}} 2 (d - x) (-1)$

$\Leftrightarrow 0 = \frac{1}{c_1} \frac{x}{\sqrt{a^2+x^2}} - \frac{1}{c_2} \frac{d-x}{\sqrt{(d-x)^2+b^2}}$

Durch geometrische Betrachtungen erkennt man:

$\Leftrightarrow 0 = \frac{1}{c_1} \sin{\alpha} - \frac{1}{c_2} \sin{\beta}$

$\Leftrightarrow \frac{c_2}{c_1} = \frac{\sin{\beta}}{\sin{\alpha}}$

(Ohne Beweis: Es ist die minimale Laufzeit)

Lichtstrahlen folgen diesem Brechungsgesetz, weil es der schnellste Weg von P₀ nach P₂ ist.

Es stellt sich die berechtigte Frage, woher das Licht im Voraus weiß, welches der schnellste Weg ist. Die Quantenmechanik liefert darauf folgende Antwort:

Es probiert sie alle aus, und zwar gleichzeitig.

Vereinfacht kann man sagen, die Beiträge aller Alternativ-Wege löschen sich durch inkohärente Überlagerung aus.

Herleitung des Reflexionsgesetzes

Herleitung des Reflexionsgesetzes

Ebenso wie das Brechungsgesetz lässt sich auch das Reflexionsgesetz mit Hilfe des Fermatschen Prinzip herleiten.

In der rechten Abbildung legt der Lichtstrahl den Weg von links A₁ = ( − a,a) nach rechts A₂ = (a,a) über P = (x,0) zurück. Da der Strahl immer in einem (homogenen) Medium bleibt gilt immer die Lichtgeschwindigkeit c.

Damit ergibt sich für die Laufzeit:

$t(x) = t_1 + t_2 = \frac{s_1}{c} + \frac{s_2}{c} = \frac{|P - A_1|}{c} + \frac{|A_2 - P|}{c} = \frac{1}{c} \left( \sqrt{(x+a)^2+a^2} + \sqrt{(a-x)^2+a^2} \right)$

Durch Ableiten nach x finden wir den Extremalwerte von t.

$0 \stackrel{!}{=} \frac{dt}{dx} = \frac{1}{c} \left( \frac{1}{2} \frac{1}{\sqrt{(x+a)^2+a^2}} 2 (x + a) + \frac{1}{2} \frac{1}{\sqrt{(a-x)^2+a^2}} 2 (a - x) (-1) \right)$

$\Leftrightarrow 0 = \frac{a+x}{\sqrt{(x+a)^2+a^2}} - \frac{a-x}{\sqrt{(a-x)^2+a^2}}$

Durch geometrische Betrachtungen erkennt man:

$\Leftrightarrow 0 = \sin{\alpha} - \sin{\beta}$

$\Leftrightarrow \sin{\alpha} = \sin{\beta}$

Nach Reihenentwicklung des Sinus erhält man:

α = β

(Ohne Beweis: Es ist die minimale Laufzeit)

Lichtstrahlen folgen diesem Reflexionsgesetz, weil es der schnellste Weg von A₁ nach A₂ ist.

Allgemeine Mathematische Formulierung

Mathematisch beschrieben, durchläuft das Licht in einem Medium, mit der Brechzahl $n(\vec{x})$, von allen denkbaren Bahnen $X:t'\mapsto \vec{x}(t')$ zwischen zwei Punkten $\vec{x}(t_1)$ und $\vec{x}(t_2)$ genau die Bahn, auf der die Laufzeit

$t[X] = \frac{1}{c}\,\int_{t_1}^{t_2} n(\vec{x}(t'))\, \sqrt{\left(\frac{\mathrm d \vec{x}(t')}{\mathrm d t'}\right)^2}\, \mathrm d t'$

stationär ist. Die Größe t ist Lichtlaufzeit zwischen beiden Punkten. Dies entspricht dem Hamiltonschen Prinzip der stationären Wirkung.

Darstellung des Fermatschen Prinzips am Beispiel einer Ellipse

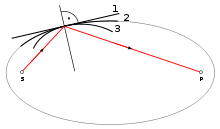
Meist ist die Lichtlaufzeit ein Minimum, das heißt: Jede kleine Änderung der Bahn vergrößert die Laufzeit. Dies muss aber nicht immer so sein, wie die rechte Abbildung zeigt. Für eine Bahn zwischen den zwei Brennpunkten S und P einer Ellipse sind drei mögliche Fälle eingezeichnet. Für eine beliebige Oberfläche am Rand dieser Ellipse gilt:

1. Bei Reflexion an einer Fläche mit einer geringeren Krümmung als jene der Ellipsoidfläche ist die Laufzeit minimal.
2. Bei Reflexion an der Ellipsoidfläche sind alle Punkte auf der Fläche gleichwertig: Bei Verschieben des Reflexionspunkts auf der Ellipsoidfläche ändert sich die Laufzeit nicht.
3. Bei Reflexion an einer Fläche mit einer größeren Krümmung als jene der Ellipsoidfläche ist die Laufdauer, verglichen mit anderen Reflexionspunkten auf dieser Fläche, maximal. Dies tritt zum Beispiel bei Reflexion an einem Hohlspiegel auf.

Siehe auch

• Hamiltonsches Prinzip

Literatur

• Florian Scheck: Theoretische Physik 3. Klassische Feldtheorie. ISBN 3540422765 (Kapitel 4.4 Geometrische Optik, 4.4.3 Medien mit negativem Brechungsindex).
• Roger Erb: Geometrische Optik mit dem Fermat-Prinzip. In: Physik in der Schule. 30, Nr. 9, 1992, S. 291–295.