Fläche zweiter Ordnung

Als Flächen zweiter Ordnung, auch Quadrik, bezeichnet man algebraische Flächen, die durch ein quadratisches Polynom beschrieben werden. Diese Punktmengen erfüllen in Koordinatenform folgende Gleichung:

a₁₁x² + a₂₂y² + a₃₃z² + 2a₁₂xy + 2a₁₃xz + 2a₂₃yz + a₁x + a₂y + a₃z + β = 0

In Matrizenschreibweise:

${\vec x}^T \cdot A \cdot \vec x + {\vec a}^T \vec x + \beta = 0$

mit

$\vec x = (x,y,z), \vec a = (a_1,a_2,a_3), A = \begin{pmatrix} a_{11} ~ a_{12} ~ a_{13} \\ a_{21} ~ a_{22} ~ a_{23} \\ a_{31} ~ a_{32} ~ a_{33} \end{pmatrix} , a_{ij} = a_{ji}$

Transformation auf Normalform:

Das singuläre Gebilde S einer Fläche zweiter Ordnung ist die Menge aller 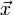$\vec x$, für die gilt:

$\vec x \cdot A = - \vec a$

Verschiebung des Koordinatensystems um einen Vektor 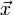$\vec x$ aus S führt zum Verschwinden der linearen Glieder in der Gleichung der Fläche zweiter Ordnung. Die Gleichung geht über in:

b₁₁x'² + b₂₂y'² + b₃₃z'² + 2b₁₂x'y' + 2b₁₃x'z' + 2b₂₃y'z' + b = 0

x',y',z' sind die Koordinaten des neuen Koordinatensystems.

Der Ursprung des neuen Koordinatensystems ist der Symmetriepunkt der Fläche 2. Ordnung.

Eine Hauptachsentransformation in ein Koordinatensystem mit festem Ursprung und Koordinatenachsen in Richtung der Eigenvektoren bringt die Gleichung der Fläche zweiter Ordnung in die Normalform:

λ₁x² + λ₂y² + λ₃z² + d = 0

Klassifizierung der Flächen zweiter Ordnung

λ1	λ2	λ3	d	Typ
>0	>0	>0	<0	Ellipsoid
>0	>0	>0	>0	nullteilige Fläche 2. Ordnung (d. h. die leere Punktmenge)
>0	>0	>0	=0	entartetes Ellipsoid (Nullpunkt) Kegel mit nichtreellen Erzeugenden
>0	>0	<0	<0	einschaliges Hyperboloid
>0	>0	<0	>0	zweischaliges Hyperboloid
>0	>0	<0	=0	elliptischer Doppelkegel (Kegelachse: x3)
>0	>0	=0	>0	Zylinder mit nichtreellen Erzeugenden
>0	>0	=0	<0	elliptischer Zylinder
>0	>0	=0	=0	Paar einander (in einer reellen Geraden) schneidender nichtreeller Ebenen
>0	<0	=0	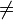$\ne$0	Hyperbolischer Zylinder
>0	<0	=0	=0	Paar sich schneidender Ebenen (beide zur z-Achse parallel)
>0	=0	=0	<0	2 parallele Ebenen (zur x-Achse parallel)
>0	=0	=0	>0	2 nichtreelle parallele Ebenen
>0	=0	=0	=0	Koordinatenebene (y,z-Ebene)