Hyperboloid

Ein Hyperboloid ist eine Fläche zweiter Ordnung, die durch Ebenen in Hyperbeln, Ellipsen, Parabeln geschnitten werden kann.

Es wird zwischen ein- und zweischaligen Hyperboloiden unterschieden, ihr gemeinsamer Grenzfall ist der Doppelkegel.

Einschaliges Hyperboloid

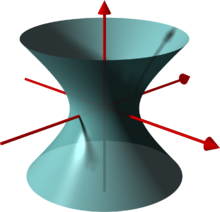
einschaliges Hyperboloid

Das einschalige Hyperboloid gleicht einem Kühlturm, auf der Oberfläche liegen zwei Scharen von Geraden. Daher ist das einschalige Hyperboloid eine Regelfläche. Jede Tangentialebene T schneidet das Hyperboloid in zwei Geraden, deren Schnittpunkt der Berührpunkt von T ist.

Formel: $\frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 1$

Ein einschaliges Hyperboloid mit a = b wird auch als Rotationshyperboloid bezeichnet.

Zweischaliges Hyperboloid

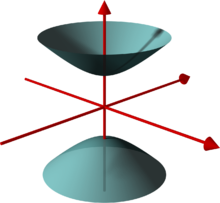
zweischaliges Hyperboloid

Das zweischalige Hyperboloid besteht aus zwei nicht miteinander verbundenen Teilflächen, es enthält keine reellen Geraden.

Formel: $\frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = -1$

Doppelkegel

Doppelkegel

Der Grenzfall zwischen ein- und zweischaligen Hyperboloiden, wenn sich die beiden Schalen in einem Punkt berühren, ist der Doppelkegel:

Formel: $\frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 0$

Parametrisierung

Es gibt verschiedene Möglichkeiten ein Hyperboloid mit einer Funktion $f: \; \mathbb R^2 \rightarrow \mathbb R^3$ zu parametrisieren. Eine einfache Möglichkeit ist die folgende, wobei d = 1 ein einschaliges, d = − 1 ein zweischaliges Hyperboloid und d = 0 einen Doppelkegel liefert:

$f: \; (s,t) \mapsto \left(a \cdot \sqrt{d+s^2} \cdot \cos(t) \,; \ b \cdot \sqrt{d+s^2} \cdot \sin(t) \,; \ c\cdot s \right)$.

Weblinks

• Animiertes Hyperboloid bei EXOPAS

 Commons: Hyperboloid – Sammlung von Bildern, Videos und Audiodateien