Formale Begriffsanalyse

Ein formaler Kontext zu Eigenschaften der Zahlen 1-10.

Begriffsverband zum obigen Zahlenkontext.

Die Formale Begriffsanalyse (FBA, englisch formal concept analysis, FCA) ist eine mathematische Theorie aus dem Gebiet der Algebra. Sie wurde bereits 1940 von Garrett Birkhoff begründet und seit 1982 von der Darmstädter Gruppe um Rudolf Wille weiterentwickelt. Der Gegenstand der formalen Begriffsanalyse sind binäre Relationen und zu ihnen in enger Verbindung stehende vollständige Verbände. Anwendungen der formalen Begriffsanalyse untersuchen Relationen aus ihrem Gebiet mittels der Begriffsanalyse. Die Ergebnisse in Form von Verbänden werden dann im Bereich der Anwendung interpretiert und können zu neuen Einsichten verhelfen.

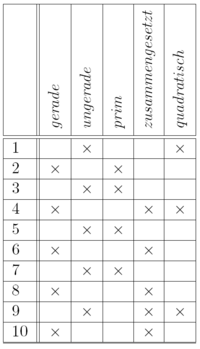
Mathematische Grundlage für die Formale Begriffsanalyse ist ein formaler Kontext K: = (G,M,I), wobei G eine Menge von Gegenständen, M eine Menge von Merkmalen und I eine Inzidenzrelation ist, so dass ein Gegenstand g aus der Gegenstandsmenge G in Relation I zu einem Merkmal m aus der Merkmalsmenge steht, wenn der Gegenstand g das Merkmal m besitzt, man schreibt: gIm.

Solche (einwertigen) Kontexte finden sich als binäre Datentabellen in vielen Lebensbereichen wieder. Beliebige Datentabellen mit endlicher Menge der vorkommenden Werte können als mehrwertige Kontexte aufgefasst und mittels sogenannter Skalierung in einwertige Kontexte übersetzt werden.

Aus diesen (einwertigen) formalen Kontexten lassen sich nun die formalen Begriffe ableiten. Die Begriffe sind dabei Zusammenfassungen von Gegenständen und Merkmalen zu größeren Einheiten ("Makros") in einer ganz bestimmten Weise: So besteht ein Begriff immer aus einem Umfang (einer Menge von Gegenständen) und einem Inhalt (einer Menge von Merkmalen), und zwar genau so, dass alle Gegenstände erfasst werden, die die ausgewählten Merkmale gemeinsam haben, und auch alle Merkmale genommen werden, die den Gegenständen gemeinsam sind.

Etwas formaler: Ein formaler Begriff ist ein Paar (A,B) mit A Teilmenge der Gegenstandsmenge G und B Teilmenge der Merkmalsmenge M. Außerdem müssen die folgenden Abschlusseigenschaften gelten: A' = B und A = B', wobei die Ableitungsoperatoren folgendermaßen definiert sind:

$A' = \{ m \in M | \; gIm \; \forall g \in A \}$ und dual $B' = \{ g \in G | \; gIm \; \forall m \in B \}$.

Die daraus resultierenden Begriffe können mit der Oberbegriffs-Unterbegriffs-Ordnung natürlich geordnet werden, wobei ein Oberbegriff immer einen größeren Umfang (und einen kleineren Inhalt) als der Unterbegriff hat.

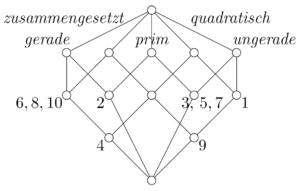
Die Sammlung aller Begriffe ergibt mit der eben beschriebenen Ordnung die mathematische Struktur eines vollständigen Verbandes. Solche Verbände können als Liniendiagramm (Hasse-Diagramm) dargestellt werden und entfalten so die Daten in ihrer Struktur und ihren Zusammenhängen. Die Gegenstände haben dabei alle (durch Kanten verbundene) darüber stehenden Merkmale; in nebenstehendem Beispiel ist 4 gerade, zusammengesetzt und quadratisch.

Die Begriffsinhalte und damit der Begriffsverband sind durch eine minimale und vollständige Menge von Implikationen eindeutig bestimmt, die sogenannte Stammbasis. Ein häufig verwendeter interaktiver Algorithmus, um diese zu bestimmen, ist die Merkmalexploration.

Die Formale Begriffsanalyse lässt sich als qualitative Methode zur Datenanalyse einsetzen. Eine direkte Anwendung ist es, die ursprünglichen Daten anders zu strukturieren und zu visualisieren.

Literatur

• Bernhard Ganter, Rudolf Wille: Formale Begriffsanalyse; Springer, 1996, ISBN 3-540-60868-0
• Bernhard Ganter, Gerd Stumme, Rudolf Wille (Hg.): Formal Concept Analysis. Foundations and Applications; Springer, 2005, ISBN 3-540-27891-5
• R. Missaoui, Jürg Schmid: Formal Concept Analysis; Springer, 2006, ISBN 3-540-32203-5
• Raoul Medina, Sergei Obiedkov (Hg.): Formal Concept Analysis. 6th International Conference, ICFCA 2008, Montreal, Canada, February 25-28, 2008, LNCS/LNAI 4933; Springer, Heidelberg 2008, ISBN 978-3-540-78136-3. Online-Version

Weblinks

• Homepage der Formalen Begriffsanalyse
• Seite der TU Dresden zur Formalen Begriffsanalyse (englisch)
• Literatur und Weblinks nicht nur zu FBA (social bookmarking)