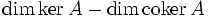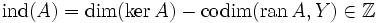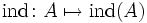- Fredholm-Index
-
In der Funktionalanalysis, einem Teilgebiet der Mathematik, ist der Begriff des Fredholm-Operators (nach E. I. Fredholm) eine Verallgemeinerung der Invertierbarkeit einer linearen Abbildung zwischen Vektorräumen. Für Fredholm-Operatoren kann der Fredholm-Index
definiert werden, der ein Spezialfall der Euler-Charakteristik ist.
Definition
Ein beschränkter linearer Operator
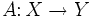 zwischen zwei Banachräumen X und Y heißt ein Fredholm-Operator, oder man sagt kurz: "A ist Fredholm", wenn
zwischen zwei Banachräumen X und Y heißt ein Fredholm-Operator, oder man sagt kurz: "A ist Fredholm", wenn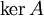 endliche Dimension hat und
endliche Dimension hat und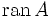 endliche Kodimension in Y hat.
endliche Kodimension in Y hat.
Dabei ist
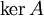 der Kern von A, also die Menge
der Kern von A, also die Menge 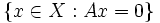 und
und 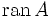 ist das Bild von A, also die Teilmenge
ist das Bild von A, also die Teilmenge 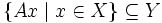 .
.Die Zahl
heißt Fredholm-Index von A.
Eigenschaften
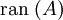 ist ein abgeschlossener Unterraum.
ist ein abgeschlossener Unterraum.- Die Abbildung
-
- ist stetig bezüglich der Operatornorm und daher wegen der Diskretheit von
 konstant auf Zusammenhangskomponenten.
konstant auf Zusammenhangskomponenten.
- Ein Operator
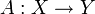 ist genau dann ein Fredholm-Operator, wenn es Operatoren B1,B2 und kompakte Operatoren K1,K2 gibt, so dass AB1 = IY − K1 und B2A = IX − K2 gilt, d.h. wenn A modulo kompakter Operatoren invertierbar ist. Insbesondere ist ein beschränkter Operator
ist genau dann ein Fredholm-Operator, wenn es Operatoren B1,B2 und kompakte Operatoren K1,K2 gibt, so dass AB1 = IY − K1 und B2A = IX − K2 gilt, d.h. wenn A modulo kompakter Operatoren invertierbar ist. Insbesondere ist ein beschränkter Operator 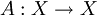 genau dann ein Fredholm Operator, wenn seine Klasse
genau dann ein Fredholm Operator, wenn seine Klasse ![[A]_{\mathcal{C}(X)}](/pictures/dewiki/54/6051ccb090674ce6b5e65895c38f3408.png) in der Calkin-Algebra
in der Calkin-Algebra 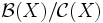 invertierbar ist.
invertierbar ist. - Für jeden Fredholm-Operator A und jeden kompakten Operator K ist A + K ebenfalls ein Fredholm-Operator mit selbem Fredholm-Index wie A. Insbesondere ist jede kompakte Störung der Identität, also jeder Operator der Form I + K für einen kompakten Operator K ein Fredholm-Operator vom Index 0.
- Ist
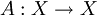 ein Fredholm-Operator, dann gibt es ein
ein Fredholm-Operator, dann gibt es ein  , so dass für alle
, so dass für alle 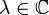 mit
mit 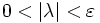 gilt
gilt
(i) A − λI ist ein Fredholm-Operator;
(ii)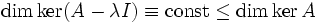 ;
;
(iii)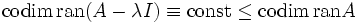 ;
;
(iv) ind(A − λI) = ind(A).
Dieser Satz heißt auch das Punctured Neighbourhood Theorem.
Wikimedia Foundation.