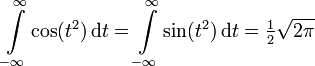Fresnelintegral

Als Fresnel-Integrale werden in der Mathematik die beiden uneigentlichen Integrale

$\int\limits_{-\infty}^{\infty}\cos(t^2)\,\mathrm{d}t =\int\limits_{-\infty}^{\infty}\sin(t^2)\,\mathrm{d}t = \tfrac12\sqrt{2\pi}$

bezeichnet; sie ergeben sich aus dem gaußschen Fehlerintegral unter Benutzung des cauchyschen Integralsatzes. Fresnel kannte sie um 1819. Euler kannte schon 1781 die allgemeineren Integrale

$\int\limits_{-\infty}^{\infty}e^{(a^2-1)t^2}\cos(2at^2)\,\mathrm{d}t =\frac{\sqrt{\pi}}{1+a^2},\qquad -1\le a\le1,$

$\int\limits_{-\infty}^{\infty}e^{(a^2-1)t^2}\sin(2at^2)\,\mathrm{d}t = \frac{a\,\sqrt{\pi}}{1+a^2},\qquad -1\le a\le1.$

Sie spielen auch eine wichtige Rolle in der Optik und Quantenmechanik.

Der Ansatz, die Quantenmechanik aus Pfadintegralen herzuleiten, basiert auf Integralen der Form:

$\mathcal{F}^{(j)}\equiv \mathcal{N} \int\limits_{-\infty}^{\infty} \ \mathrm{e}^{i \alpha \xi^2} \xi^j \mathrm{d}\xi$

Eine praktische Formulierung der Normierungskonstante 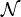$\mathcal{N}$ ist

$\mathcal{N} \equiv \sqrt{\frac{\alpha}{i\pi}}$,

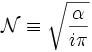j ist eine ganze natürliche Zahl.

Für j = 0 ist das Integral

$\mathcal{F}\equiv \mathcal{F}^{(0)} \equiv \mathcal{N} \int\limits_{-\infty}^{\infty} \ \mathrm{e}^{i \alpha \xi^2} \mathrm{d}\xi$

und heißt dann Fresnel-Integral. Integrale dieser Form tauchen in der aus den feynmanschen Pfadintegralen hergeleiteten Schrödingergleichung auf.

Aus dem Fresnelintegral ergibt sich eine komplexe Zahl, deren Real- und Imaginärteile bestimmt sind durch:

$\int\limits_{-\infty}^{\infty} \, \cos (\alpha \xi^2) = \sqrt{\frac{\pi}{2\left|\alpha\right|}}\mathrm{d}\xi$ und

$\int\limits_{-\infty}^{\infty} \, \sin (\alpha \xi^2) = \sqrt{\frac{\pi}{2\left|\alpha\right|}}\cdot \operatorname{sign}(\alpha)\mathrm{d}\xi$

Beide Integrale konvergieren. Das Cosinus-Integral ist aufgrund der Symmetrie des Cosinus invariant gegenüber einem Vorzeichenwechsel von α, der antisymmetrische Sinus wechselt das Vorzeichen.

Aus der Addition ergibt sich mit 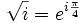$\sqrt{i}=e^{i\frac{\pi}{4}}$, − 1 = eⁱπ und einer Fallunterscheidung für die Signum-Funktion als Lösung des Fresnel-Integrals

$\mathcal{F}\equiv \mathcal{F}^{(0)} \equiv \mathcal{N} \int\limits_{-\infty}^{\infty} \ \mathrm{e}^{i \alpha \xi^2} \mathrm{d}\xi = \sqrt{\frac{\alpha}{i\pi}}\cdot \sqrt{\frac{i\pi}{\alpha}}=1$.

Hieraus erklärt sich auch die Normierungskonstante, die genau das Inverse der Integrallösung sein muss, damit der Gesamtausdruck 1 ist. In der Quantenmechanik wählt man dies aus pragmatischen Gründen und aus der Idee heraus, dass eine Wellenfunktion einer Aufenthaltswahrscheinlichkeit entspricht; also muss das Integral über diese Funktion 1 sein, da sich das beschriebene Teilchen schließlich irgendwo befindet.

Literatur

• Reinhold Remmert, Georg Schumacher: Funktionentheorie 1. 5. Auflage, Springer-Verlag 2002, ISBN 3540590757, Seiten 156f.
• Reinhold Remmert, Georg Schumacher: Funktionentheorie 2. 3. Auflage, Springer-Verlag 2007, ISBN 3540404325, Seite 47.