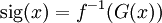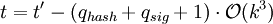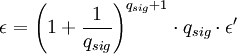- Full Domain Hash
-
Full-Domain-Hash (Abk.: FDH) ist ein Signaturverfahren aus dem Bereich der Kryptologie. Der Empfänger einer Nachricht kann damit überprüfen, ob die Nachricht, die der Absender an ihn gesandt hat, durch einen Dritten verändert wurde oder nicht.
Das Prinzip das Verfahrens besteht darin, eine Nachricht zuerst zu hashen und anschließend zu verschlüsseln. Als Hashfunktion verwendet man ein Zufallsorakel, das alle Werte aus dem Definitionsbereich der Verschlüsselungsfunktion erzeugen kann. Daher kommt auch der Name Full-Domain-Hash. Als Verschlüsselungsfunktion wird eine beliebige Trapdoor-Einwegpermutation verwendet.
Das Optimal-Asymmetric-Encryption-Padding ist unter den Verschlüsselungsverfahren das Analogon zum Full-Domain-Hash.
Inhaltsverzeichnis
Beschreibung des Protokolls
Das Full-Domain-Hash-Verfahren ist ein asymmetrisches Signaturverfahren dessen öffentlicher Schlüssel (f,G) aus einer Trapdoor-Einwegpermutation
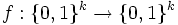 und einem Zufallsorakel
und einem Zufallsorakel 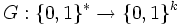 gebildet wird. Der zugehörige geheime Schlüssel ist die Umkehrfunktion f − 1 der Trapdoor-Einwegpermutation.
gebildet wird. Der zugehörige geheime Schlüssel ist die Umkehrfunktion f − 1 der Trapdoor-Einwegpermutation.Die Signatur einer Nachricht x wird durch folgende Funktion berechnet:
Die Nachricht wird dann zusammen mit der Signatur an den Empfänger gesandt.
Der Empfänger erhält die Nachricht x zusammen mit der Signatur
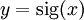 . Mit der Verifikationsfunktion
. Mit der Verifikationsfunktionüberprüft er die Nachricht. Diese gibt genau dann wahr aus, wenn die Nachricht nicht verändert wurde.
RSA-Full-Domain-Hash
Verwendet man als Trapdoor-Einwegpermutation f die RSA-Funktion f(x) = xemod N mit den von RSA bekannten Parametern, dann spricht man vom RSA-Full-Domain-Hash. Das Verfahren ist nachweislich sicher, das heißt es kann auch mit einem Angriff mit frei wählbarem Klartext keine existenzielle Fälschung erzeugt werden.
Sicherheit des RSA-Full-Domain-Hash
Wenn RSA (t',ε')-sicher ist, dann ist das RSA-Full-Domain-Hash-Verfahren auf Basis des Zufallsorakel-Modells (t,ε)-sicher mit
Beachte, dass der Artikel von Jean-Sébastien Coron offenbar qsig > 0 voraussetzt. Für große qsig läuft dies auf
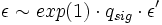 hinaus.
hinaus.Das bedeutet: Wenn es einen Algorithmus gibt, der eine existenzielle Fälschung für das Full-Domain-Hash-Verfahren mit einer Laufzeit von t und Erfolgswahrscheinlichkeit von ε erstellen kann und dabei höchstens qhash berechnet und höchstens qsig Unterschriften benötigt, dann gibt es einen Algorithmus, der diskrete Logarithmen von RSA-Modulen mit einer Laufzeit von t' und Erfolgswahrscheinlichkeit von ε' berechnet.
Quellen
- Douglas R. Stinson: Cryptography. Theory and Practice. 3. Auflage. Chapman & Hall/CRC, 2005, ISBN 1-58488-508-4, S. 304–307
- Jean-Sébastien Coron: On the Exact Security of Full Domain Hash. CRYPTO 2000: S. 229–235
- Mihir Bellare, Phillip Rogaway: The Exact Security of Digital Signatures – How to Sign with RSA and Rabin. EUROCRYPT 1996: S. 399–416
Wikimedia Foundation.