Gerda Ganzer — Gerda Ganzer, geborene Quernheim, (* 15. Dezember 1907 in Oberhausen; † unbekannt) war Häftlingskrankenschwester im KZ Ravensbrück. Leben Gerda Ganzer absolvierte nach dem Abschluss des Lyzeums eine kaufmännische Lehre und danach ihre Ausbildung… … Deutsch Wikipedia
Dedekind-Ring — Ein Dedekindring (nach Richard Dedekind, auch ZPI Ring) ist eine Verallgemeinerung des Ringes der ganzen Zahlen. Die Anwendungen dieses Begriffes finden sich hauptsächlich in den mathematischen Teilgebieten der algebraischen Zahlentheorie und der … Deutsch Wikipedia
ZPI-Ring — Ein Dedekindring (nach Richard Dedekind, auch ZPI Ring) ist eine Verallgemeinerung des Ringes der ganzen Zahlen. Die Anwendungen dieses Begriffes finden sich hauptsächlich in den mathematischen Teilgebieten der algebraischen Zahlentheorie und der … Deutsch Wikipedia
Verzweigte Körpererweiterung — Verzweigung ist ein mathematischer Begriff, der die Gebiete Algebra, algebraische Geometrie und komplexe Analysis miteinander verbindet. Inhaltsverzeichnis 1 Namengebendes Beispiel 2 Verzweigung im Kontext von Erweiterungen bewerteter Körper 2.1… … Deutsch Wikipedia
Verzweigungspunkt — Verzweigung ist ein mathematischer Begriff, der die Gebiete Algebra, algebraische Geometrie und komplexe Analysis miteinander verbindet. Inhaltsverzeichnis 1 Namengebendes Beispiel 2 Verzweigung im Kontext von Erweiterungen bewerteter Körper 2.1… … Deutsch Wikipedia
Ganzzahlring — Im mathematischen Teilgebiet der algebraischen Zahlentheorie ist der Ganzheitsring eines algebraischen Zahlkörpers das Analogon des Ringes der ganzen Zahlen im Fall des Körpers der rationalen Zahlen. Definition Es sei K ein algebraischer… … Deutsch Wikipedia
Kathedrale von Nevers — Martyrium des hl. Quiricus und der hl. Julitta, 15. Jahrhundert … Deutsch Wikipedia
Ste-Eulalie-et-Ste-Julie d’Elne — Die heutige Pfarrkirche Sainte Eulalie et Sainte Julie (katalanisch Santa Eulàlia d Elna) ist eine im 11. Jahrhundert errichtete, im 13. bis 15. Jahrhundert erweiterte ehemalige Kathedrale in der südfranzösischen Stadt Elne (Pyrénées Orientales,… … Deutsch Wikipedia
St-Jacques de Neuvy-Saint-Sépulchre — Stiftskirche Neuvy Saint Sépulchre, von O … Deutsch Wikipedia
Gerda Quernheim — Gerda Ganzer, geborene Quernheim, (* 15. Dezember 1907 in Oberhausen; † unbekannt) war Häftlingskrankenschwester im KZ Ravensbrück. Leben Gerda Ganzer absolvierte nach dem Abschluss des Lyzeums eine kaufmännische Lehre und danach ihre Ausbildung… … Deutsch Wikipedia
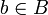 ganz über A, wenn es ein normiertes Polynom
ganz über A, wenn es ein normiertes Polynom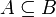 , so spricht man von einer ganzen Ringerweiterung.
, so spricht man von einer ganzen Ringerweiterung.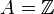 und
und 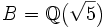 , so ist der ganze Abschluss von A in B gleich
, so ist der ganze Abschluss von A in B gleich
![p=X^n+c_{n-1}X^{n-1}+\ldots+c_1X+c_0\in A[X]](/pictures/dewiki/98/b87c961d9679e6a9e1f098081357fed5.png)
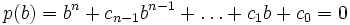
![\mathbb Z\!\left[\frac{1+\sqrt5}2\right].](/pictures/dewiki/102/f632f6672eab286873f00dfeea28628f.png)