Ganzzahlring

Im mathematischen Teilgebiet der algebraischen Zahlentheorie ist der Ganzheitsring eines algebraischen Zahlkörpers das Analogon des Ringes der ganzen Zahlen im Fall des Körpers der rationalen Zahlen.

Definition

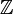Es sei K ein algebraischer Zahlkörper, d.h. eine endliche Erweiterung des Körpers der rationalen Zahlen. Dann ist der Ganzheitsring $\mathcal O_K$ von K definiert als der ganze Abschluss von $\mathbb Z$ in K, d.h. die Teilmenge derjenigen 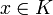$x\in K$, die eine Gleichung der Form

$x^n + c_{n-1}x^{n-1} + \ldots + c_1 x + c_0 = 0$

mit $c_i\in\mathbb Z$ erfüllen. Man beachte, dass der Koeffizient von xⁿ gleich 1 sein muss.

Eine äquivalente Definition lautet: Der Ganzheitsring von K ist die im Sinne der Inklusion maximale Ordnung, die Hauptordnung auf K.

Eigenschaften

• $\mathcal O_K$ ist ein Dedekindring.

Beispiele

• Ist $K=\mathbb Q(\mathrm i\sqrt3)$, so ist $\mathcal O_K$ der Ring der Eisenstein-Zahlen

$u + v\cdot\frac{-1+\mathrm i\sqrt3}2$ mit $u,v\in\mathbb Z.$

Eine solche Zahl ist Nullstelle des Polynoms

X² − (2u − v)X + (u² − uv + v²).

Erfüllt umgekehrt $x=a+b\mathrm i\sqrt3\in K$ die Polynomgleichung

x² + px + q = 0 mit $p,q\in\mathbb Z,$

so folgt p = − 2a und q = a² + 3b². Man kann zeigen, dass daraus folgt, dass a + b und 2b ganzzahlig sind, also ist

$x = (a+b) + 2b\cdot\frac{-1+\mathrm i\sqrt3}2$

eine Eisenstein-Zahl.

• Ist $K=\mathbb Q(\mathrm i)$, so ist $\mathcal O_K$ der Ring der ganzen gaußschen Zahlen $\mathbb Z[\mathrm i]$.

• Allgemein sieht für den Ganzheitsring von $\mathbb Q(\sqrt{d})$ (wobei d ganz und quadratfrei sei) eine Ganzheitsbasis so aus:

$\{1,\sqrt{d} \}$ falls d kongruent 2 oder 3 mod 4

$\{1, \frac{1+\sqrt{d}}2 \}$ falls d kongruent 1 mod 4

• Bezeichnet ζ eine primitive n-te Einheitswurzel, so ist der Ganzheitsring des n-ten Kreisteilungskörpers $\mathbb Q(\zeta)$ gleich $\mathbb Z[\zeta]$.