ZPI-Ring

Ein Dedekindring (nach Richard Dedekind, auch ZPI-Ring) ist eine Verallgemeinerung des Ringes der ganzen Zahlen. Die Anwendungen dieses Begriffes finden sich hauptsächlich in den mathematischen Teilgebieten der algebraischen Zahlentheorie und der kommutativen Algebra, besonders in der Idealtheorie.

Definition

Ein Dedekindring ist ein höchstens eindimensionaler, noetherscher, normaler Integritätsbereich.

Eigenschaften

Analog zur eindeutigen Zerlegung ganzer Zahlen in Primzahlen gilt für Dedekindringe, dass in ihnen jedes Ideal eine eindeutige Zerlegung in Primideale besitzt. Dedekindringe sind gerade diejenigen Integritätsbereiche, die ZPI-Ringe sind.

Beispiele

• Jeder Hauptidealring ist ein Dedekindring.
• Ist A ein Hauptidealring, und L eine endliche Erweiterung seines Quotientenkörpers, so ist der ganze Abschluss von A in L ein Dedekindring. Insbesondere gilt das für Ganzheitsringe in Zahlkörpern, also beispielsweise $\mathbb Z[\sqrt{-5}].$
• Lokalisierungen von Dedekindringen sind wieder Dedekindringe.

Keine Dedekindringe sind:

• $\mathbb Z[T]$ (zweidimensional),
• $\mathbb Z[\sqrt5]$ (nicht normal),
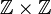• $\mathbb Z[T]/(T^2)$ oder $\mathbb Z\times\mathbb Z$ (kein Integritätsbereich).