Gauss-Prozess

Ein stochastischer Prozess 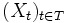$(X_t)_{t \in T}$ auf einer beliebigen Indexmenge T wird Gauß-Prozess (nach Carl Friedrich Gauß) genannt, wenn seine endlichdimensionalen Verteilungen (mehrdimensionale) Normalverteilungen (auch Gauß-Verteilungen, daher der Name) sind. Es soll also für alle 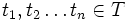$t_1, t_2 \ldots t_n \in T$ die multivariate Verteilung von 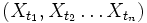$(X_{t_1}, X_{t_2} \ldots X_{t_n})$ durch eine n-dimensionale Normalverteilung gegeben sein.

Eine besondere Eigenschaft der Gauß-Prozesse ist von der Normalverteilung geerbt, die durch ihre ersten zwei Momente bereits eindeutig bestimmt ist: So haben zwei Gauß-Prozesse, die über dieselbe Erwartungswertfunktion 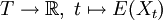$T \to \mathbb{R}, \; t \mapsto E(X_t)$ und Kovarianzfunktion 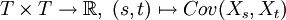$T \times T \to \mathbb{R}, \; (s,t) \mapsto Cov(X_s,X_t)$ verfügen, dieselbe Verteilung.

Ein Gauß-Prozess heißt zentriert, wenn sein Erwartungswert konstant 0, die Erwartungswertfunktion also die Nullfunktion ist.

Beispiele

• Der Wiener-Prozess (bzw. Brownsche Bewegung) hat Erwartungswertfunktion 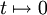$t \mapsto 0$ und Kovarianzfunktion $(s,t) \mapsto min(s,t)$.

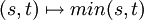• Das Gauß'sche weiße Rauschen hat Erwartungswert 0 und Kovarianzfunktion 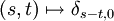$(s,t) \mapsto \delta_{s-t,0}$ (Dirac-Funktion)

• Ist 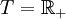$T=\mathbb{R}_{+}$ und f,g zwei integrierbare reellwertige Funktionen sowie W ein Wiener-Prozess, so ist der Itō-Prozess 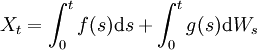$X_t= \int_0^t f(s) \mathrm ds+ \int_0^t g(s) \mathrm dW_s$ ein Gauß-Prozess mit Erwartungswertfunktion 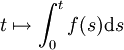$t \mapsto \int_0^t f(s) \mathrm ds$ und Kovarianzfunktion $(s,t) \mapsto \int_0^{min(s,t)} g^2(r) \mathrm dr$.

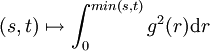Literatur

• R. M. Dudley, Real Analysis and Probability, Wadsworth and Brooks/Cole, 1989.
• B. Simon, Functional Integration and Quantum Physics, Academic Press, 1979.
• C. E. Rasmussen, C. K. I. Williams, Gaussian Processes for Machine Learning, MIT Press, 2006. ISBN 0-262-18253-X
• M.L. Stein, Interpolation of Spatial Data: Some Theory for Kriging, Springer, 1999

Weblinks

• Gaussian Processes Web Site (inkl. Tutorials, Code etc.)