- Gehaltsgröße
-
Gehaltsangaben – auch Gehaltsgrößen genannt – geben in Chemie und Physik den Gehalt eines Stoffes in einem Stoffgemisch an, quantifizieren also einen materiellen Anteil eines Stoffes an einem Gemisch, beispielsweise einer Lösung. Sie werden gemacht in Bezug auf die Größen:
- Masse m,
- Volumen V oder
- Stoffmenge n.
Möglich, aber weniger üblich ist, den Gehalt mit Hilfe von Teilchenzahlen anzugeben. Alle Gehaltsgrößen, die den Volumenbegriff enthalten, sind temperaturabhängig. Zu einer eindeutigen Angabe von Konzentrationen, Volumenanteilen und Volumenverhältnissen gehört daher auch die Nennung der zugehörigen Temperatur.
Es existieren daher Angaben als:
- Anteile in Bezug auf die Summen der Einzelkomponenten – z. B. gelöste Stoffe und Lösungsmittel (Massenanteil, Stoffmengenanteil, Volumenanteil)
- Konzentrationen in Bezug auf das Volumen der Mischung oder Lösung (Massenkonzentration, Stoffmengenkonzentration, Volumenkonzentration)
- Verhältnisse in Bezug z. B. auf das Lösungsmittel (Massenverhältnis, Stoffmengenverhältnis, Volumenverhältnis).
Diese Gehaltsangaben / Gehaltsgrößen werden für eine Lösung (Lsg) vom Stoff (i bzw. j) im Lösemittel (LM) z. B. folgendermaßen definiert:
Inhaltsverzeichnis
Angabe des Anteils einer Komponente
Massenanteil:
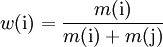
Stoffmengenanteil:
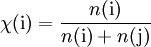
Volumenanteil:
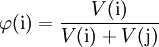
- Die Angabe „Masse%“ entspricht dem Massenanteil x100, die Angabe „Volumen%“ der Volumenanteil x100. Diese Bezeichnungsweisen sind unsystematisch, aber noch nicht völlig ausgestorben; denn Prozent ist nichts Anderes als eine andere Schreibfigur für die Zahl 0,01.
- Neben Angaben in Prozent (1 %= 1:100 Teile) der Gesamtmasse oder des Gesamtvolumens von Lösung und Gemisch existieren noch Angaben in Promille (1 : 1000), ppm (1 : 1 Million), ppb (1 : 1 Milliarde), ppt (1 : 1 Billion) und ppq (1 : 1 Billiarde); jedoch sind solche Bezeichnungen – außer Prozent und Promille – nicht empfehlenswert, siehe parts per million.
- V(Gemisch) bzw. V(Lösung) ist die Summe der Volumina der Einzelkomponenten vor oder nach dem Lösevorgang bzw. der Mischung. Ist das Volumen des Gemisches V(Lösung) nicht gleich der Summe der Volumina V(i) + V(LM) vor dem Mischen, so tritt beim Mischen der Komponenten eine Volumenkontraktion oder evtl. auch eine Volumenausdehnung Volumendilatation ein.
- Bei einer Volumenkontraktion gilt also: V(i) + V(LM) > V(Lösung). Daher müssen Volumenanteil φ(i) (in Bezug auf die Summe der Einzelvolumina der Stoffe) und Volumenkonzentration σ(i) (in Bezug auf das Volumen der Lösung nach dem Lösen/Mischen) voneinander unterschieden werden. Oft ist die Angabe des Volumenanteils daher unzweckmäßig, besser ist statt dessen, die Volumenkonzentration anzugeben.
- Für ideale Gase i gilt φ(i) = x(i).
Angabe der Konzentration einer Komponente
Massenkonzentration:
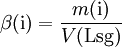
Stoffmengenkonzentration:
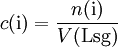
Volumenkonzentration:
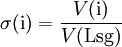
(Vgl. Anmerkung zum Volumenanteil oben)
Molalität (veraltet):
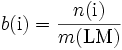
(Neben diesem Begriff existiert in der Chemie noch die ebenfalls veraltete „Gehaltsangabe“ Normalität. Hier hat man die Stoffmengenkonzentration c = n/V (Molarität) mit der chemischen stöchiometrischen Wertigkeit z des reagierenden Stoffes multipliziert. Eine Schwefelsäure mit c = 0,5 mol/L hat daher z. B. die Normalität 1,0. In DIN-normgerechter Darstellung bedeutet dies Folgendes: Legt man bei der Verwendung des Mol Schwefelsäure-Teilchen H2SO4 zu Grunde, ist c = 0,5 mol/L, legt man stattdessen Äquivalent-Teilchen 1/2 (H2SO4) zu Grunde, weil im Falle der betrachteten chemischen Reaktion die stöchiometrische Wertigkeit der Schwefelsäure z = 2 beträgt, ist c = 1 mol/L; in veralteter Sprechweise: eine 0,5-molare wässerige Schwefelsäurelösung ist 1-normal, sofern die Schwefelsäure 2-wertig benutzt wird.)
Angabe des Verhältnisses zweier Komponenten
Massenverhältnis:
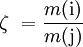
Stoffmengenverhältnis:
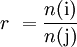
Volumenverhältnis:.
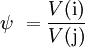
Umrechnung
Zur Umrechnung der Gehaltsangaben benötigt man insbesondere folgende Größen:
- M = m / n (Molare Masse = Masse / Stoffmenge)
- ρ = m / V (Dichte = Masse / Volumen)
- Vm = V / n (Molares Volumen = Volumen / Stoffmenge).
Siehe auch
Massenanteil, Massenprozent, Stoffkonzentration, Stoffmengenkonzentration, Massenkonzentration, Volumenkonzentration, Volumenanteil, Stoffmengenanteil, Massenverhältnis, Volumenverhältnis, Stoffmengenverhältnis
Wikimedia Foundation.
