Gesetz der grossen Zahlen

Gesetz der großen Zahlen ist eine Bezeichnung für bestimmte mathematische Sätze aus der Stochastik. In ihrer einfachsten Form besagen diese Sätze, dass die relative Häufigkeit eines Zufallsergebnisses im Sinne eines stochastischen Konvergenzbegriffs gegen die Wahrscheinlichkeit des Zufallsergebnisses konvergiert, wenn das Zufallsexperiment immer wieder durchgeführt wird.

Beispiel: Wurf einer Münze

Die Wahrscheinlichkeit, dass eine Münze beim Werfen Kopf zeigt, betrage ½. Je häufiger die Münze geworfen wird, desto unwahrscheinlicher ist es dann, dass der Anteil der Würfe, bei denen Kopf erscheint, um mehr als ein beliebig vorgegebenes ε > 0 vom theoretischen Wert ½ abweicht. Demgegenüber ist durchaus wahrscheinlich, dass die absolute Differenz zwischen der Anzahl der Kopf-Würfe und der halben Gesamtzahl der Würfe anwächst.

Das Gesetz der großen Zahlen bedeutet also nicht, dass ein Ereignis, welches bislang nicht so häufig eintrat wie erwartet, seinen „Rückstand“ irgendwann ausgleichen und folglich in Zukunft häufiger eintreten muss. Dies ist ein bei Roulette- und Lottospielern häufig verbreiteter Irrtum, die „säumige“ Zahlenart müsse nun aber aufholen, um wieder der statistischen Gleichverteilung zu entsprechen.

Praktische Bedeutung

• Versicherungswesen: Das Gesetz der großen Zahlen hat bei Versicherungen eine große praktische Bedeutung. Es erlaubt eine ungefähre Vorhersage über den künftigen Schadensverlauf. Je größer die Zahl der versicherten Personen, Güter und Sachwerte, die von der gleichen Gefahr bedroht sind, desto geringer ist der Einfluss des Zufalls. Das Gesetz der großen Zahlen kann aber nichts darüber aussagen, wer im einzelnen von einem Schaden getroffen wird. Unvorhersehbare Großereignisse und Trends wie der Klimawandel, die die Berechnungsbasis von Durchschnittswerten verändern, können das Gesetz zumindest teilweise unbrauchbar machen.
• Medizin: Beim Wirksamkeitsnachweis von medizinischen Verfahren kann man es nutzen, um Zufallseinflüsse auszuschalten.
• Naturwissenschaften: Der Einfluss von (nicht systematischen) Messfehlern kann durch häufige Versuchwiederholungen reduziert werden.

Siehe auch: Gesetz der kleinen Zahlen

Schwaches Gesetz der großen Zahlen

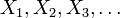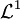Man sagt, eine Folge von Zufallsvariablen $X_1, X_2, X_3, \dots$ in $\mathcal{L}^1$ genüge dem schwachen Gesetz der großen Zahlen, wenn für 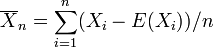$\overline{X}_n=\sum_{i=1}^{n}(X_i-E ( {X}_i ))/n$ für alle positiven Zahlen $\varepsilon$ gilt:

$\lim_{n\rightarrow\infty}\operatorname{P}\left(\left|\overline{X}_n\right|>\varepsilon\right)=0$.

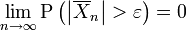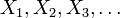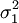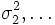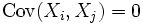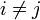Es gibt verschiedene Voraussetzungen, unter denen das schwache Gesetz der großen Zahlen gilt. Es gilt beispielsweise, wenn die Zufallsvariablen $X_1, X_2, X_3, \dots$ endliche Varianzen $\sigma_1^2$,$\sigma_2^2,\dots$ besitzen, die zudem durch eine gemeinsame obere Grenze beschränkt sind, und jeweils paarweise unkorreliert sind, also $\operatorname{Cov}(X_i, X_j) = 0$ für $i\neq j$ erfüllen.^[1]

Das schwache Gesetz der großen Zahlen von Chintschin nennt als Bedingung für die stochastische Konvergenz, dass die Zufallsvariablen einer Folge 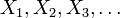$X_1, X_2, X_3, \dots$ unabhängig und identisch verteilt sind und einen endlichen Erwartungswert besitzen.^[2][3]

Der Beweis der genannten Sätze lässt sich jeweils über die Tschebyschow-Ungleichung führen.

Starkes Gesetz der großen Zahlen

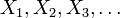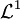Man sagt, eine Folge von Zufallsvariablen $X_1, X_2, X_3, \dots$ in $\mathcal{L}^1$ genüge dem starken Gesetz der großen Zahlen, wenn für 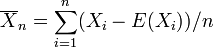$\overline{X}_n=\sum_{i=1}^{n}(X_i-E ( {X}_i ))/n$ gilt:

$\operatorname{P}\left(\limsup_{n\rightarrow\infty}|\overline{X}_n|=0\right)=1$.

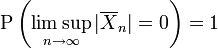Das starke Gesetz der großen Zahlen impliziert das schwache Gesetz der großen Zahlen.

Ein starkes Gesetz der großen Zahlen gilt beispielsweise, wenn die Folge unabhängig ist und die Zufallsvariablen identisch verteilt sind. Eine Form des starken Gesetzes der großen Zahlen für abhängige Zufallsvariablen ist der Ergodensatz.

Die Geschichte des starken Gesetzes der großen Zahlen ist lang. Sie hat mit dem Satz von N. Etemadi^[4] 1981 einen gewissen Abschluss gefunden. Der Satz von Etemadi zeigt die Gültigkeit des starken Gesetzes der großen Zahlen unter der Annahme, dass die Zufallsvariablen integrierbar sind (also einen endlichen Erwartungswert besitzen), jeweils dieselbe Verteilung haben und je zwei Zufallsvariablen unabhängig sind. Die Existenz einer Varianz wird nicht vorausgesetzt.

Literatur

• H.-O. Georgii: Stochastik, 2. Auflage, de Gruyter, 2004.
• R. Durrett: Probability: Theory and Examples, 3rd ed., Duxbury, 2004.

Einzelnachweise

1. ↑ H.-O. Georgii: Stochastik, 2. Auflage, de Gruyter, 2004, S. 120 Satz (5.6) Schwaches Gesetz der großen Zahlen, $\mathcal L^2$-Version.
2. ↑ Marek Fisz: Wahrscheinlichkeitsrechnung und mathematische Statistik. Deutscher Verlag der Wissenschaften, Berlin 1989, S 260 Satz 6.11.4 ( Chintschin)
3. ↑ H.-O. Georgii: Stochastik, 2. Auflage, de Gruyter, 2004, S. 121 Satz (5.7) Schwaches Gesetz der großen Zahlen, $\mathcal L^1$-Version.
4. ↑ Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete (jetzt: Probability Theory and Related Fields), Band 55(1), S. 119-122, (1981)