Gewichtetes harmonisches Mittel
- Gewichtetes harmonisches Mittel
-
Das harmonische Mittel ist ein Mittelwert einer Menge von Zahlen. Das harmonische Mittel der Zahlen 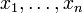 ist definiert als
ist definiert als
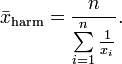
Durch Bildung des Kehrwertes erhält man
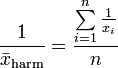 ,
,
der Kehrwert des harmonischen Mittels ist also das arithmetische Mittel der Kehrwerte.
Für zwei Werte a und b ergibt sich
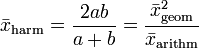
Beispiel für das harmonische Mittel von 5 und 20:
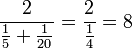
oder
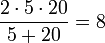
Mit dieser Formel ist das harmonische Mittel zunächst nur für von Null verschiedene Zahlen xi definiert. Geht aber einer der Werte xi gegen Null, so existiert der Grenzwert des harmonischen Mittels und ist ebenfalls gleich Null. Daher ist es sinnvoll, das harmonische Mittel als Null zu definieren, wenn mindestens eine der zu mittelnden Größen gleich Null ist.
Gewichtetes harmonisches Mittel
Sind den xi positive Gewichte wi > 0 zu geordnet so ist das gewichtete harmonisches Mittel wie folgt definiert:
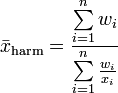
Sind alle wi = 1 so erhält man das gewöhnliche harmonische Mittel.
Beispiel
Allgemein gilt: Benötigt man für die Teilstrecke s1 die Zeit t1 (also Durchschnittsgeschwindigkeit v1 = s1 / t1) und für die Teilstrecke s2 die Zeit t2 (also Durchschnittsgeschwindigkeit v2 = s2 / t2, so gilt für die Durchschnittsgeschwindigkeit über die gesamte Strecke
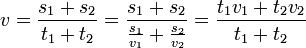
Die Durchschnittsgeschwindigkeit ist also das mit den Wegstrecken gewichtete harmonische Mittel der Teilgeschwindigkeiten oder das mit der benötigten Zeit gewichtete arithmetische Mittel der Teilgeschwindigkeiten.
Fährt man eine Stunde mit 50 km/h und dann eine Stunde mit 100 km/h, so legt man insgesamt 150 km in 2 Stunden zurück; die Durchschnittsgeschwindigkeit ist 75 km/h, also das arithmetische Mittel von 50 und 100. Bezieht man sich hingegen nicht auf die benötigte Zeit, sondern auf die durchfahrene Strecke, so wird die Durchschnittsgeschwindigkeit durch das harmonische Mittel beschrieben: Fährt man 100 km mit 50 km/h und dann 100 km mit 100 km/h, so legt man 200 km in 3 Stunden zurück, die Durchschnittsgeschwindigkeit ist 66 2/3 km/h, also das harmonische Mittel von 50 und 100.
![v=\frac{100+100}{2+1}=\frac{100+100}{\frac{100}{50}+\frac{100}{100}}=\frac{1*100+1*100}{2+1}=\frac{200}{3}=66~2/3~[km/h]](/pictures/dewiki/57/977dfd1c7b4dbeefa7f354d356413f07.png)
Weblinks
Eric W. Weisstein: Harmonic Mean auf MathWorld (englisch)
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Harmonisches Mittel — Das harmonische Mittel ist ein Mittelwert einer Menge von Zahlen und wird typischerweise für die Mittelwertbildung von Anteilswerten oder Prozentzahlen genutzt. Das harmonische Mittel der Zahlen ist definiert als Durch Bildung des Kehrwertes… … Deutsch Wikipedia
Gewichtetes geometrisches Mittel — Das geometrische Mittel ist ein Mittelwert; es ist in der Statistik ein geeignetes Mittelmaß für Größen, von denen das Produkt anstelle der Summe interpretierbar ist, z. B. von Verhältnissen oder Wachstumsraten. Inhaltsverzeichnis 1 Definition 2… … Deutsch Wikipedia
Gewichtetes Mittel — Mittelwerte treten in der Mathematik und insbesondere in der Statistik in inhaltlich unterschiedlichen Kontexten auf. In der Statistik ist ein Mittelwert ein sog. Lageparameter (Überbegriff Parameter (Statistik)), also ein aggregierender… … Deutsch Wikipedia
Gewogenes arithmetisches Mittel — Mittelwerte treten in der Mathematik und insbesondere in der Statistik in inhaltlich unterschiedlichen Kontexten auf. In der Statistik ist ein Mittelwert ein sog. Lageparameter (Überbegriff Parameter (Statistik)), also ein aggregierender… … Deutsch Wikipedia
Hölder'sches Mittel — Mittelwerte treten in der Mathematik und insbesondere in der Statistik in inhaltlich unterschiedlichen Kontexten auf. In der Statistik ist ein Mittelwert ein sog. Lageparameter (Überbegriff Parameter (Statistik)), also ein aggregierender… … Deutsch Wikipedia
Höldersches Mittel — Mittelwerte treten in der Mathematik und insbesondere in der Statistik in inhaltlich unterschiedlichen Kontexten auf. In der Statistik ist ein Mittelwert ein sog. Lageparameter (Überbegriff Parameter (Statistik)), also ein aggregierender… … Deutsch Wikipedia
Winsorisiertes Mittel — Mittelwerte treten in der Mathematik und insbesondere in der Statistik in inhaltlich unterschiedlichen Kontexten auf. In der Statistik ist ein Mittelwert ein sog. Lageparameter (Überbegriff Parameter (Statistik)), also ein aggregierender… … Deutsch Wikipedia
Hölder-Mittel — In der Mathematik ist das Hölder Mittel oder der Höldersche Mittelwert (nach Otto Hölder, 1859–1937) (engl. u.A. (p th) power mean) ein (manchmal auch der) verallgemeinerte Mittelwert. Die Bezeichnung ist uneinheitlich, Bezeichnungen wie das p te … Deutsch Wikipedia
Geometrisches Mittel — Das geometrische Mittel ist ein Mittelwert; es ist in der Statistik ein geeignetes Mittelmaß für Größen, von denen das Produkt anstelle der Summe interpretierbar ist, z. B. von Verhältnissen oder Wachstumsraten. Inhaltsverzeichnis 1… … Deutsch Wikipedia
Gemittelt — Mittelwerte treten in der Mathematik und insbesondere in der Statistik in inhaltlich unterschiedlichen Kontexten auf. In der Statistik ist ein Mittelwert ein sog. Lageparameter (Überbegriff Parameter (Statistik)), also ein aggregierender… … Deutsch Wikipedia
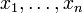 ist definiert als
ist definiert als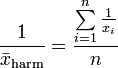 ,
,
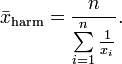
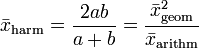
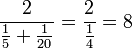
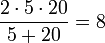
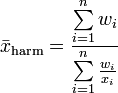
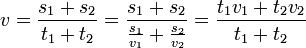
![v=\frac{100+100}{2+1}=\frac{100+100}{\frac{100}{50}+\frac{100}{100}}=\frac{1*100+1*100}{2+1}=\frac{200}{3}=66~2/3~[km/h]](/pictures/dewiki/57/977dfd1c7b4dbeefa7f354d356413f07.png)