- Gewichtetes geometrisches Mittel
-
Das geometrische Mittel ist ein Mittelwert; es ist in der Statistik ein geeignetes Mittelmaß für Größen, von denen das Produkt anstelle der Summe interpretierbar ist, z. B. von Verhältnissen oder Wachstumsraten.
Inhaltsverzeichnis
Definition
Das geometrische Mittel der n Zahlen
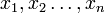 ist gegeben durch die n-te Wurzel des Produkts der n Zahlen:
ist gegeben durch die n-te Wurzel des Produkts der n Zahlen:Eigenschaften
Im Gegensatz zum arithmetischen Mittel ist das geometrische Mittel nur für nichtnegative, Zahlen xi definiert und meistens nur für echt positive reelle Zahlen sinnvoll, denn wenn ein Faktor gleich null ist, ist schon das ganze Produkt gleich null und für komplexe Zahlen wird es nicht eingesetzt, da die komplexen Wurzeln mehrdeutig sind.
Die Ungleichung vom arithmetischen und geometrischen Mittel besagt, dass das geometrische Mittel nie größer als das arithmetische Mittel ist. Äquivalent dazu gilt:
das heißt der Logarithmus des geometrischen Mittels ist das arithmetische Mittel der Logarithmen, wobei die Basis des Logarithmus beliebig gewählt werden darf, aber auf beiden Seiten die gleiche sein muss.
Analog zum gewichteten arithmetischen Mittel lässt sich ein mit den Gewichten wi > 0 gewichtetes geometrisches Mittel definieren:
wobei
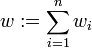 . Das arithmetisch-geometrische Mittel ist eine Zahl, die zwischen dem arithmetischen und geometrischen Mittel liegt.
. Das arithmetisch-geometrische Mittel ist eine Zahl, die zwischen dem arithmetischen und geometrischen Mittel liegt.Außerdem gilt
mit dem arithmetischen und dem harmonischen Mittel.
Anwendungsbeispiele
- Das geometrische Mittel von 3 und 300:
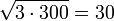
- Das Mittel aus einer Verdopplung und nachfolgender Verachtfachung einer Bakterienkultur ist eine Vervierfachung (nicht eine Vermehrung um den Faktor 5).
- Ein Guthaben G wird im ersten Jahr mit zwei Prozent, im zweiten Jahr mit sieben und im dritten Jahr mit fünf Prozent verzinst. Welcher über die drei Jahre konstante Zinssatz p hätte zum Schluss das gleiche Kapital ergeben?
Guthaben GEnde am Ende des dritten Jahres:
oder mit Zinsfaktoren geschrieben
Mit konstantem Zinssatz p und zugehörigen Zinsfaktor 1 + p ergibt sich am Ende ein Guthaben von
Mit Gkonst = GEnde ergibt sich
und damit berechnet sich der durchschnittliche Zinsfaktor 1 + p zu
Der durchschnittliche Zinssatz beträgt also ca.
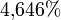 . Allgemein berechnet sich der durchschnittliche Zinsfaktor also aus dem geometrischen Mittel der Zinsfaktoren der einzelnen Jahre. Wegen der Ungleichung vom arithmetischen und geometrischen Mittel ist der durchschnittliche Zinssatz kleiner oder bestenfalls gleich dem arithmetischen Mittel der Zinssätze, welches in diesem Beispiel
. Allgemein berechnet sich der durchschnittliche Zinsfaktor also aus dem geometrischen Mittel der Zinsfaktoren der einzelnen Jahre. Wegen der Ungleichung vom arithmetischen und geometrischen Mittel ist der durchschnittliche Zinssatz kleiner oder bestenfalls gleich dem arithmetischen Mittel der Zinssätze, welches in diesem Beispiel 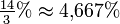 beträgt.
beträgt.Geometrische Interpretation
Das geometrische Mittel zweier Zahlen a und b liefert die Seitenlänge eines Quadrates, das den gleichen Flächeninhalt hat wie das Rechteck mit den Seitenlängen a und b. Genauso entspricht es bei drei Zahlen der Seite eines Würfels der volumengleich ist zu dem Quader mit den drei Seitenlängen und entsprechend im n-dimensionalen bei n Zahlen mittels Hyperwürfeln.
Weblinks
- Eric W. Weisstein: Geometric Mean auf MathWorld (englisch)
Wikimedia Foundation.

![G(x_1,x_2\ldots,x_n)= \bar{x}_\mathrm{geom} = \sqrt[n]{\prod_{i=1}^n{x_i}} = \sqrt[n]{x_1 \cdot x_2 \cdot \ldots \cdot x_n}](/pictures/dewiki/57/97227bea3fa3401d08ee313359c38240.png)
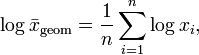
![\bar{x}_\mathrm{geom} = \sqrt[w]{\prod_{i=1}^n x_i^{w_i}}](/pictures/dewiki/54/6f34a214fd3b345ef92496418e75d21f.png)
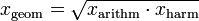
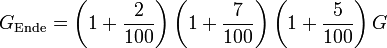
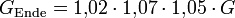
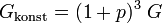
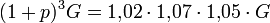
![1+p=\sqrt[3]{1{,}02 \cdot 1{,}07 \cdot 1{,}05}\approx 1{,}04646](/pictures/dewiki/102/f90aa86f1c878aa7fd47dfb7d7923b7e.png)