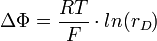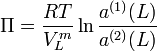Gibbs-Donnan-Effekt

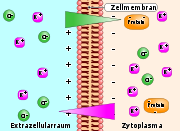Schematische Darstellung des Donnan-Gleichgewichts über eine Zellmembran

Das Donnan-Gleichgewicht beschreibt in der Physikalischen Chemie die ungleiche Verteilung von gelösten geladenen Teilchen (Ionen), die sich einstellt, wenn eine semipermeable Membran für das Lösungsmittel und einige, nicht aber alle in der Lösung vorhandenen Ionen durchlässig ist. In diesem Fall verteilen sich die passierenden Ionen auf beiden Seiten der Membran in unterschiedlicher Konzentration. Diese Ungleichverteilung führt zu einer Potentialdifferenz (Donnan-Potential oder besser: Donnan-Spannung) und einer Differenz des osmotischen Drucks (Donnan-Druck). Das Ausmaß der Abweichung wird durch den Donnan-Koeffizient angegeben.

Benannt ist dieser Effekt nach dem Chemiker Frederick George Donnan, der 1911 eine Theorie zur Erklärung solcher Membrangleichgewichte aufgestellt hat. Die Konzentrationsverteilung wird daher als Donnan-Gleichgewicht (auch Gibbs-Donnan-Gleichgewicht), der zugrundeliegende Vorgang als Gibbs-Donnan-Effekt oder Donnan-Gesetz bezeichnet. Das Donnan-Prinzip besagt, dass auf jeder Seite der Membran die Ladungen aller beteiligten Ionen ausgeglichen (Null) sein muss.

Der Donnan-Effekt ist insbesondere für lebende Zellen aber auch für technische Systeme von Bedeutung.

Grundlagen

Voraussetzung für das Auftreten des Gibbs-Donnan-Effekts ist die Anwesenheit einer Ionensorte, die von der semipermeablen Membran nicht durchgelassen wird. Dies ist regelmäßig bei Makromolekülen wie löslichen Proteinen oder Nukleinsäuren in biologischen Zellen der Fall. Bei entsprechender Membranbeschaffenheit kann dies aber auch für eine Ionensorte eines niedermolekularen Salzes zutreffen. So ist bei gelöstem Natriumchlorid (Kochsalz) der Durchmesser des hydratisierten Cl⁻-Ions erheblich größer als der des kleineren Na⁺-Ions.^[1] Zum Donnan-Effekt kommt es auch, wenn Ionen durch Verankerung an einer Grenzfläche nicht frei diffundieren können, wie dies bei Membranproteinen oder geladenen Polymermolekülen (siehe Ionentauscher) der Fall ist.

Ein osmotisches System ist im Gleichgewicht, wenn die chemischen Potentiale des Lösungsmittels und der anderen durchgelassenen Stoffe auf beiden Seiten der Membran jeweils gleich sind. Bei Anwesenheit von Ladungsträgern müssen als zusätzliche Bedingung die elektrische Ladungen auf beiden Seiten ausgeglichen sein (Donnan-Bedingung). Ist daher auf einer Seite der Membran eine nicht permeierende Ionensorte stärker konzentriert, kann der Ladungsüberschuss nur durch entgegengesetzt geladene Ionen neutralisiert werden, die die Membran passieren können. Deren Konzentration (genauer Aktivität) ist daher im Gleichgewicht auf beiden Seiten unterschiedlich. Aufgrund dieser Ungleichverteilung tritt eine Potentialdifferenz im Bereich einiger Millivolt (mV) auf. Führt die Ungleichverteilung zu einer Differenz der Aktivität des Wassers, entsteht ein osmotischer Druck.

Donnan-Koeffizient

Wie stark die tatsächliche Ionenverteilung von einer Gleichverteilung abweicht, gibt der Donnan-Koeffizient an. Sind in einem System auf beiden Seiten _a,_i der Membran permeable, einwertige Ionen K⁺ (Kalium) und Cl^- (Chlorid) vorhanden sowie auf Seite _i ein Makromolekül mit z Ladungen P^z+, so gilt die Donnan-Bedingung (ausgeglichene Ladungssumme):

$[K^+]_a \, - \, [Cl^-]_a \, = \, 0$

sowie

$[K^+]_i \, - \, [Cl^-]_i \, + \!\,\, z[P^{z+}]_i= \, 0$

Im Gleichgewicht gilt für die Verteilung der durchgelassen Ionen:

$r_D \, = \, \frac{[K^+]_a}{[K^+]_i} \, = \, \frac{[Cl^-]_i}{[Cl^-]_a}$

Dabei ist r_D der Donnan-Koeffizient, eine dimensionslose Zahl. Bei Gleichverteilung hat sie den Wert 1; in Anwesenheit nicht permeabler Ionen nimmt r_D einen Wert größer als 1 an. Die Zusammenhang zwischen Donnan-Koeffizient und Konzentration des geladenen Makromoleküls wird für verdünnte Lösungen in guter Näherung durch die Formel

$r_D \!\,\ \approx \ 1 + \frac{z\cdot[P^{z+}]_i}{2\cdot[K^+]_i}$

beschrieben.^[2] Sie besagt, dass die durchgelassenen Ionen umso ungleicher verteilt sind, je höher Konzentration und Anzahl der Ladungen eines nichtpermeierenden Makromoleküls sind. Zudem wird eine Abhängigkeit des Donnan-Koeffizienten vom pH-Wert der Lösung erkennbar: Da der Dissoziationsgrad eines Makromoleküls (insbesondere bei ampholytischen Proteinen) vom pH-Wert der Lösung abhängt, wirkt sich eine Änderung des pH-Werts über die Änderung der Ladungszahl z auch auf die Verteilung der kleinen, durchgelassenen Ionen aus.

Donnan-Potential

Der Zusammenhang zwischen Membranpotential und Donnan-Koeffizient ergibt sich aus der Nernst-Gleichung:

$\Delta\Phi = \frac{RT}{F} \cdot ln (r_D)$

ΔΦ ist die Differenz des elektrischen Potentials in mV, R die universelle Gaskonstante, T die absolute Temperatur in K und F die Faraday-Konstante in C · mol⁻¹.

Die nachfolgende Tabelle zeigt, dass die Anwesenheit eines nicht permeablen Ions zu großen Konzentrationsunterschieden bei den durchgelassenen Ionen führen kann. Gleichzeitig können beträchtliche Donnan-Potentiale auftreten:^[2]

z·[Pz+]i	[K+]a = [Cl-]a	[Cl-]i	[K+]i	rD	ΔΦ (mV)[3]
0,002	0,0010	0,00041	0,00241	2,44	22,90
	0,0100	0,00905	0,01105	1,10	2,56
	0,1000	0,0990	0,1010	1,01	2,58
0,02	0,0010	0,00005	0,02005	20,05	76,96
	0,0100	0,00414	0,02414	2,41	22,65
	0,1000	0,0905	0,1105	1,10	2,56

(alle Konzentrationsangaben in mol·l^-1). Die Höhe des Membranpotentials hängt vom Verhältnis des geladenen Makromoleküls zu den beweglichen Ionen ab. Sind solche Ionen in hoher Konzentration vorhanden, wirkt sich die Anwesenheit des unbeweglichen Ions nur geringfügig aus.

Osmotischer Druck

Im Gleichgewicht ergibt sich der osmotische Druck aus Verhältnis der Aktivitäten des Lösungsmittel auf beiden Seiten der Membran:

$\Pi = \frac{RT}{V^m_L} \ln \frac{a^{(1)}(L)}{a^{(2)}(L)}\!\,$

Dabei sind: 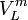$V^m_L$ das Molvolumen des Lösungsmittels, R die universelle Gaskonstante und T die absolute Temperatur in K.

Siehe auch

• Goldman-Gleichung
• Kolloidosmotischer Druck

Einzelnachweise und Literatur

1. ↑ Sehon Hannes. Physikalische Chemie. Verlag Herder Freiburg. i. Brsg. 1976, ISBN 3-451-16411-6
2. ↑ ^{a b} Moore Walter J., Hummel Dieter O.: Physikalische Chemie, S. 650f. Walter de Gruyter, Berlin 1986, ISBN 3-110-10979-4.
3. ↑ Charles Tanford. Physical Chemistry of Macromolecules. John Wiley, New York 1961.

• Moore Walter J., Hummel Dieter O.: Physikalische Chemie. Walter de Gruyter, Berlin 1986, ISBN 3-110-10979-4.

Weblinks

• Vorlesungsskript Biophysik der Uni Rostock (PDF)
• Membranpotential bei Universität Hamburg Botanik online