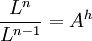Hack (Begriffsklärung) — Hack bezeichnet: Hack, einen Begriff aus dem Computerslang Hack (Computerspiel), ein Rogue ähnliches Computerspiel von 1985 Eine Aktion des Hackens Hack (Pferd), eine Turnierpferdart .hack, eine Multimediareihe (Anime, Manga und Videospiel) die… … Deutsch Wikipedia
Gesetz von Hack — Das Hacksche Gesetz stammt aus dem Jahre 1957 [J.T. Hack (1957)] und beschreibt in der Hydrologie die fraktale Längen Flächen Relation von Einzugsgebieten. Es gibt ein Verhältnis zwischen Gewässerlänge (Hauptgerinne) und Einzugsgebietsgröße. Bei… … Deutsch Wikipedia
Hack'sches Gesetz — Das Hacksche Gesetz stammt aus dem Jahre 1957 [J.T. Hack (1957)] und beschreibt in der Hydrologie die fraktale Längen Flächen Relation von Einzugsgebieten. Es gibt ein Verhältnis zwischen Gewässerlänge (Hauptgerinne) und Einzugsgebietsgröße. Bei… … Deutsch Wikipedia
Hacksches Gesetz — Das Hacksche Gesetz stammt aus dem Jahre 1957 [J.T. Hack (1957)] und beschreibt in der Hydrologie die fraktale Längen Flächen Relation von Einzugsgebieten. Es gibt ein Verhältnis zwischen Gewässerlänge (Hauptgerinne) und Einzugsgebietsgröße. Bei… … Deutsch Wikipedia
0190-Dialer — Dialer (deutsch: Einwahlprogramme) sind im engeren Sinne Computerprogramme, mit deren Hilfe über das analoge Telefon oder das ISDN Netz eine Wählverbindung zum Internet oder anderen Computernetzwerken aufgebaut werden kann. So ist bei vielen… … Deutsch Wikipedia
Einwahlprogramm — Dialer (deutsch: Einwahlprogramme) sind im engeren Sinne Computerprogramme, mit deren Hilfe über das analoge Telefon oder das ISDN Netz eine Wählverbindung zum Internet oder anderen Computernetzwerken aufgebaut werden kann. So ist bei vielen… … Deutsch Wikipedia
Geschichte Myanmars — Dies ist ein Überblick über die Geschichte Birmas (auch Burma, offiziell Myanmar). Inhaltsverzeichnis 1 Königreiche Bagan, Bago, Ava und Arakan 2 Britische Herrschaft 2.1 Kolonialtruppen … Deutsch Wikipedia
Feldbereinigung — Feldbereinigung. Gemeinheitsteilung, Güterarrondierung, Güterverlegung, Güterzusammenlegung, Feldbereinigung, Flurbereinigung, Kommassation, Konsolidation, Segregation, Separation, Vereinödung, Verkuppelung sind die teils ähnlichen, teils mehr… … Lexikon der gesamten Technik
Futurezone — Die Futurezone (ehemals auch: futureZone, Abk.: fuZo) ist ein österreichisches Internetportal für Nachrichten aus dem Bereich Computer, Informationstechnik, Telekommunikation und Netzpolitik. Es wurde im Jahr 1999 vom öffentlich rechtlichen… … Deutsch Wikipedia
Liste der Comic-Publikationen des Carlsen Verlags — Als internationaler Großverlag hat der Carlsen Verlag in Hamburg seit den späten 1960er Jahren eine Vielzahl von Serien und Einzelbänden herausgegeben. Mit monatlichen Neuerscheinungen ist das Verlagsprogramm angewachsen, und nicht jede Reihe… … Deutsch Wikipedia