Heiratsproblem

Die Artikel Odds-Strategie und Sekretärinnenproblem überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese Überschneidungen. Bitte entferne diesen Baustein erst nach vollständiger Abarbeitung der Redundanz. Nichtich 21:59, 24. Feb. 2007 (CET)

In der Statistik, der Spieltheorie und der Entscheidungstheorie bezeichnet das Sekretärinnenproblem (auch bekannt als Heiratsproblem) die Zielstellung, aus einer Reihe nacheinander betrachteter Kandidaten unterschiedlicher Qualität den besten auszuwählen. Dabei ist eine Ablehnung unwiderruflich. Wegen der enthaltenen Zufallselemente wird das Problem meist so formuliert, die größte Wahrscheinlichkeit zu bestimmen, das beste Angebot auszuwählen.

Problem

Eine häufige angeführte Variante ist das Beispiel einer Organisation, die eine Sekretärin einstellen möchte. Die Bewerberinnen sprechen nacheinander vor; in der Begutachtung kann eine Rangfolge aufgestellt werden und die Qualitäten einer jeden Bewerberin können festgehalten werden. Allerdings scheidet eine abgelehnte Bewerberin endgültig aus und steht im weiteren Verlauf nicht mehr zur Verfügung, eine Prämisse, die der tatsächlichen Personalbesetzungsrealität widerspricht. Eine andere Formulierung des Problems geht von der Wahl eines Ehepartners aus einer Reihe von Kandidaten aus. Diese Problemeinkleidung ist realitätsnah – lässt man einmal die Liebe außer Betracht. Die Problemstellung schließt mit ein, dass die Wahrscheinlichkeit, den jeweils besten Bewerber auszuwählen, maximiert werden soll. Soll stattdessen der Erwartungswert bezogen auf alle in Frage kommenden Kandidaten maximiert werden, wäre eine abweichende Strategie notwendig.

Strategie

Das Problem hat eine sehr einfache Strategie, die dazu auch noch optimal ist: betrachte die ersten r der n Kandidaten mit 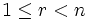$1\leq r<n$ – und lehne sie ab. Wähle von den verbleibenden n − r Bewerbern den ersten, der besser ist als jeder der ersten r. Es lässt sich zeigen, dass sich für große n der optimale Wert für r ergibt aus 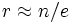$r\approx n/e$, wobei e die Basis des natürlichen Logarithmus (Eulersche Zahl) ist. Mit dieser Strategie liegt die Wahrscheinlichkeit den besten Kandidaten zu wählen bei 1 / e, also etwa 37%.

Beweis

Es sind nur zwei Bewerber von Interesse, der beste Bewerber – wir nehmen an, es sei der a-te – sowie der zweitbeste von den ersten a Bewerbern.

Wenn 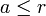$a \le r$, dann ist der beste Bewerber auch unter den pauschal abgewiesenen, womit die Strategie gescheitert ist.

Wenn der zweitbeste von den ersten a nicht zu den pauschal abgewiesenen ersten r gehört, geht er dem a-ten voran, ist zugleich besser als jeder der r ersten und wird also genommen (oder möglicherweise sogar ein anderer Bewerber vor ihm). Wieder scheitert die Strategie.

Es bleibt also der Fall, dass der zweitbeste unter den ersten a Bewerbern schon unter den ersten r Bewerbern kommt, dafür ist die Wahrscheinlichkeit 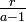$\tfrac{r}{a-1}$; dann und nur dann wird wirklich der a-te Bewerber genommen.

Der beste Bewerber liegt mit gleicher Wahrscheinlichkeit an jeder Stelle a in der Reihenfolge 1, 2, … n. Wenn man dies berücksichtigt, ergibt sich die Wahrscheinlichkeit P für einen Erfolg der Strategie zu:

$P = \sum_{a=r+1}^n \frac{1}{n} \cdot \frac{r}{a-1}$

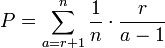
Für die Summe macht man die mit wachsendem n immer besser werdende Integral-Näherung:

$P \approx \frac{1}{n}\int_r^n \frac{r}{a}da = -\frac{r}{n}\ln\frac{r}{n}$

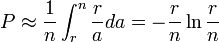
Indem man die Ableitung dieses Näherungsausdrucks gleich 0 setzt, ermittelt man dessen Maximum, es liegt an der Stelle 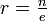$r = \tfrac{n}{e}$ und beträgt 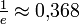$\tfrac{1}{e} \approx 0{,}368$. Das Maximum ist nicht sehr ausgeprägt, für den weiten Bereich 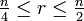$\tfrac n4 \leq r \leq \tfrac n2$ wird nämlich durchweg 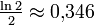$\tfrac{\ln2}{2} \approx 0{,}346$ nie unterschritten.

Anwendbarkeit in der Praxis

Die praktische Anwendbarkeit des Problemes dürfte geringer sein, als man zunächst annehmen wird. Problematisch ist zunächst, dass, um die optimale „Stoppzahl“ bestimmen zu können, von Anfang an bekannt sein muss, wie hoch n ist. Dies mag noch möglich sein, wenn eine feststehende Zahl von Bewerbungsgesprächen vereinbart ist, in der Einkleidung des Heiratsproblemes ist diese Prognose jedoch schwierig.

Weiterhin setzt das Sekretärinnenproblem voraus, dass die Qualität der Kandidaten zufällig und unabhängig von der Platzziffer ist. Auch diese Voraussetzung mag im Bewerbungsfall unter Umständen gegeben sein. Ein Gegenbeispiel ist jedoch das Heiratsproblem wie exemplarisch unter Zugrundelegung traditioneller, veralteter Rollenbilder gezeigt wird: Mit zunehmendem Alter der Frau wird die Qualität der potentiell interessierten Partner tendenziell sinken, dagegen wird bei einem zunehmenden Wohlstand des Mannes bzw. einer Verbesserung seiner gesellschaftlichen Position die Qualität seiner potentiell interessierten Partnerinnen möglicherweise steigen. Dementsprechend wäre bezüglich dieses Falles der Frau zu einer gewichteten Verringerung der Stoppzahl zu raten, dem Mann eher zu einer Erhöhung der Stoppzahl.

Ein weiteres Problem ist allerdings, dass allein aufgrund der hinausgezögerten Entscheidungsphase eine längere Zeit ohne Problemlösung überwunden werden muss, was zu Wohlfahrtsverlusten führen kann.

Eine weitere Schwierigkeit ist, dass die Lösung des Sekretärinnenproblems daraufhin optimiert ist, die beste Lösung zu wählen, wofür eine vergleichsweise hohe Wahrscheinlichkeit in Kauf genommen wird, dass schließlich die platzziffermäßig letzte, möglicherweise deutlich schlechtere Lösung in Kauf genommen werden muss. In der Praxis, in der eine derartige Optimierung hin zur besten Lösung oftmals unnötig ist, dürfte eine risikoaversere Strategie oftmals günstiger sein. Wenn also etwa bereits vor Erreichen der Stoppzahl eine Lösung als guter Kompromiss oder sogar objektiv gut erscheint, dann sollte diese Lösung in Abweichung von der Strategie sofort gewählt werden.

Varianten

Das Problem ist in verschiedenen Varianten untersucht worden, darunter:

• Die Wahl darf auf zwei Kandidaten fallen, anstatt nur auf einen.
• Die Zahl der Bewerber ist unbekannt.
• Gleichwertige Kandidaten sind von Bedeutung.
• Abgelehnte Bewerber sind nicht endgültig ausgeschieden.
• Die Wahl darf auch auf den zweitbesten Bewerber fallen.

Siehe auch

Verwandte Themen, bei denen man aus Teilinformation die optimale Entscheidung des Restproblems treffen kann:

• Gefangenenparadoxon
• Odds-Strategie
• Umtauschparadoxon
• Ziegenproblem
• Zwei-Zettel-Spiel

Für einen im Juni 2005 in Spektrum der Wissenschaft erschienen Artikel über die Odds-Strategie erhielt der Mathematiker Franz Thomas Bruss von der European Mathematical Society (EMS) den ersten Preis des Artikelwettbewerbs 2005.^[1]

Literatur

• Franz Thomas Bruss: Strategien der besten Wahl. In: Spektrum der Wissenschaft. Nr. 05, 2004, S. 102–104 (PDF). 
• Eric W. Weisstein: Sultan's Dowry Problem. In: MathWorld. Wolfram, 2004 (HTML ; Stand: 24.2.2007). 

Weblinks

• Mathematik-Online: Sekretärinnenproblem
• Lieses Verehrer oder das "Sekretärinnen-Problem"

Einzelnachweis

1. ↑ Article Competition 2005: Results. European Mathematical Society (online ; Stand: 30. November 2006).