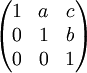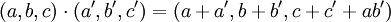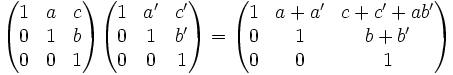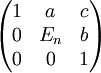Heisenberg-Gruppe

Als Heisenberggruppe bezeichnet man in der Mathematik eine bestimmte Gruppe von Matrizen sowie Verallgemeinerungen davon. Jede Heisenberggruppe besitzt eine topologische Struktur und ist eine Lie-Gruppe.

Die Heisenberggruppe wurde von Hermann Weyl eingeführt, um in der Quantenmechanik die Äquivalenz von Heisenberg-Bild und Schrödinger-Bild zu erklären.

Definition

Obere 3x3-Dreiecksmatrizen der Form

$\begin{pmatrix} 1 & a & c \\ 0 & 1 & b \\ 0 & 0 & 1 \\ \end{pmatrix}$

mit Einträgen a, b und c, die einem (beliebigen) kommutativen Ring entstammen können, bilden eine Gruppe unter der üblichen Matrizenmultiplikation, die so genannte Heisenberggruppe. Die Einträge entstammen dabei oft dem Ring der reellen Zahlen oder dem der ganzen Zahlen.

Eigenschaften

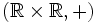Man kann die Heisenberggruppe mit Einträgen aus $\mathbb{R}$ als zentrale Erweiterung der Gruppe $(\mathbb{R}\times\mathbb{R},+)$ auffassen, was man am besten sieht, wenn man auf $\mathbb{R}^3$ durch

$(a,b,c)\cdot(a',b',c')=(a+a',b+b',c+c'+ab')$

eine Gruppenmultiplikation definiert und

$\begin{pmatrix} 1 & a & c \\ 0 & 1 & b \\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} 1 & a' & c' \\ 0 & 1 & b' \\ 0 & 0 & 1 \\ \end{pmatrix} = \begin{pmatrix} 1 & a+a' & c+c'+ab'\\ 0 & 1 & b+b' \\ 0 & 0 & 1 \\ \end{pmatrix}$

beachtet.

Lie-Algebra

Die Lie-Algebra der Heisenberggruppe ist die Heisenberg-Algebra

Anwendung

In der Quantenmechanik spielt die Heisenberggruppe die Funktion einer Symmetriegruppe.

Verallgemeinerungen

Es gibt höherdimensionale verallgemeinerte Heisenberggruppen. Als Matrizengruppe besteht die n-te Heisenberggruppe aus den quadratischen oberen Dreiecksmatrizen der Größe n + 2 der Gestalt

$\begin{pmatrix} 1 & a & c \\ 0 & E_n & b \\ 0 & 0 & 1 \\ \end{pmatrix}$

wobei a ein Zeilenvektor der Länge n, b ein Spaltenvektor der Länge n und E_n die $n \times n$-Einheitsmatrix ist.