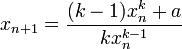- Heronverfahren
-
Das Heron-Verfahren oder babylonische Wurzelziehen ist ein Rechenverfahren zur Berechnung einer Näherung der Quadratwurzel einer Zahl. Es ist ein Spezialfall des Newton-Verfahrens.
Die Iterationsvorschrift lautet:
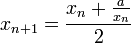 .
.
Hierbei steht a für die Zahl, deren Quadratwurzel bestimmt werden soll. Der Startwert x0 der Iteration kann, solange er nicht gleich Null ist, beliebig festgesetzt werden, wobei zu beachten ist, dass negative Werte gegen die negative Quadratwurzel konvergieren.
Inhaltsverzeichnis
Beispiel
Im Folgenden ein einfaches Beispiel für die Wurzel aus 9 und die Annäherung nach vier Berechnungsschritten an den wahren Wert
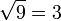
- a = 9 und x0 = 9
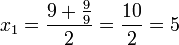
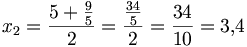
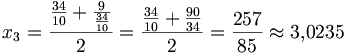
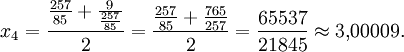
Geometrische Veranschaulichung des Heron-Verfahrens
Dem Heron-Verfahren liegt die Idee zu Grunde, dass ein Quadrat mit Flächeninhalt A eine Seitenlänge von
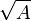 hat. Ausgangspunkt des Verfahrens ist ein beliebiges Rechteck mit Flächeninhalt A. Schritt für Schritt wird das Seitenverhältnis des Rechtecks so geändert, dass sich seine Form immer mehr der eines Quadrats annähert, während der Flächeninhalt gleich bleibt. Die Seitenlängen des Rechtecks sind die Näherungswerte für
hat. Ausgangspunkt des Verfahrens ist ein beliebiges Rechteck mit Flächeninhalt A. Schritt für Schritt wird das Seitenverhältnis des Rechtecks so geändert, dass sich seine Form immer mehr der eines Quadrats annähert, während der Flächeninhalt gleich bleibt. Die Seitenlängen des Rechtecks sind die Näherungswerte für 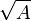 .
.Im ersten Schritt wird eine beliebige Seitenlänge x0 für das Rechteck gewählt. Damit dieses den gewünschten Flächeninhalt hat, wird die zweite Seitenlänge mit der Formel
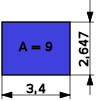
berechnet. Als Beispiel soll die Wurzel aus 9 berechnet werden. Für die eine Seitenlänge wird der Wert 9 gewählt, sodass sich die andere Seitenlänge zu 1 berechnet. Das erste Rechteck hat deshalb die folgende Form.
Die Ähnlichkeit dieses Rechteck mit einem Quadrat ist gering. Das kommt auch dadurch zum Ausdruck, dass die Seitenlängen 1 und 9 sehr schlechte Näherung für die Wurzel aus 9, deren genauer Wert 3 ist, sind.
Um eine bessere Annäherung an ein Quadrat zu erhalten, muss die lange Seite gekürzt und die kurze Seite verlängert werden. Als neue Länge der langen Seite wird der Mittelwert
der beiden bisherigen Seitenlängen genommen. Die Länge der anderen Seite berechnet sich wie oben zu
Im Beispiel ergibt sich als Mittelwert die Seitenlänge 5. Die dazugehörige kurze Seite hat eine Länge von 1,8.
Auch hier ist die Ähnlichkeit zu einem Quadrat noch gering. Allerdings ist das neue Rechteck im Vergleich zum vorhergehenden kompakter.
Der beschriebene Ablauf wird in jedem weiteren Schritt des Heron-Verfahrens wiederholt. Der Mittelwert der Seitenlängen eines Rechtecks entspricht der Länge der langen Seite des neuen Rechtecks und die Länge der kurzen Seite lässt sich daraus jeweils wie oben beschrieben berechnen. Im Beispiel entstehen so in den nächsten zwei Schritten die folgenden beiden Rechtecke.
Das letzte Rechteck ist schon annähernd quadratisch. Die Seitenlänge 3,024 liegt entsprechend nah bei 3, dem exakten Wert von
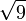 .
.Konvergenz
Es gelten: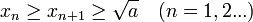 ,
,
d. h. der Näherungswert geht von oben gegen die gesuchte Wurzel, und
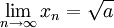 ,
,
d. h. das Verfahren konvergiert gegen die Wurzel.
Da sich das Heron-Verfahren aus dem Newtonschen Näherungsverfahren ableiten lässt, ist die Konvergenzordnung 2.
Das Verfahren konvergiert sehr schnell, wenn bereits eine gute Näherung vorliegt, d. h. es erzeugt im nächsten Schritt eine noch viel bessere Näherung. Die Zahl der richtigen Stellen wird mit jedem Schritt etwa verdoppelt. Wenn die erste Näherung jedoch schlecht ist, braucht es viele Schritte, um eine gute Näherung zu erreichen.
Wenn zum Beispiel aus einer Ganzzahl a mit 200 Binärstellen die Wurzel berechnet werden soll und man mit x0 = a als erster Näherung beginnt, dann wird die Näherung mit jedem Schritt um etwa eine Binärstelle kürzer, d. h. erst nach etwa 100 Schritten hat die Näherung die richtige Länge von 100 Stellen. Danach reichen sechs bis sieben weitere Schritte (log2(100)), um alle 100 Stellen vor dem Komma richtig zu berechnen.
Es empfiehlt sich somit, einen möglichst genauen Startwert x0 zu bestimmen. Im Beispiel sollte man zuerst die Länge von a ermitteln, und einen Startwert mit genau der halben Länge verwenden.
Fehler
Für den Fehler der Heron-Folge
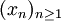 gilt:
gilt: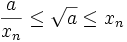 (Einschließung),
(Einschließung),
sowie
Implementierung in Software
Das Verfahren eignet sich besonders gut zur Implementierung in Software, da nur Grundrechenarten benötigt werden, s. o. Es wird heute angesichts der breiten Verfügbarkeit numerischer Prozessorhardware aber nur noch selten benötigt.
Wenn dazu noch eine Gleitkommadarstellung mit einem Zweier-Exponenten benutzt wird, wird der Ansatz relativ einfach, als Beispiel wird die Wurzel aus 5 betrachtet und der relative Fehler zum Endwert (also abs((xi - x) / x)) verfolgt:
- Zunächst wird von diesem Zweier-Exponenten eine gerade Anzahl abgespaltet, so dass als Exponent entweder eine -1 oder 0 übrig bleibt, die Zahl also auf das Intervall { ½ , 2 } normalisiert wird. In diesem Intervall ist die Wurzelfunktion eine nur schwach gekrümmte Kurve, lässt sich also numerisch gut behandeln. Beispiel:
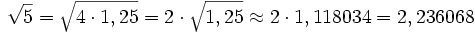 , es wird also vorerst nur noch a=1,25 mit dem Ziel x=1,118034 behandelt.
, es wird also vorerst nur noch a=1,25 mit dem Ziel x=1,118034 behandelt. - Als Startwert für die eigentliche Iteration approximiert man diese Kurve durch eine noch einfachere, die sich direkt (ohne Iteration) berechnen lässt. Mit dieser Anfangsberechnung wird der Startwert ermittelt, mit dem die folgende Iteration begonnen wird. Man kann diese Kurve mehr oder weniger aufwendig ansetzen, mit den steigend komplizierteren Ansätzen unten lässt sich ggf. ein Iterationsschritt einsparen:
- eine einfache Konstante (beispielsweise 1),
Beispiel: x0 = 1; rel. Fehler=1,1*10-1; - eine Gerade mit Steigung 1/2 und einer additiven Konstante von 1/2 (als Vereinfachung des nachfolgenden Falls),
Beispiel: x0=1/2+1,25/2=1,125; rel. Fehler=6,2*10-3; - eine Gerade mit Steigung 1/2 und einer additiven, optimierten Konstante von
![\left( 2\cdot
\sqrt[4]{2} - \sqrt{2} \right)^2 / 2 \approx 0{,}4648415](/pictures/dewiki/48/0a38a7edb9c3f4a993b8728fa467c374.png) ,
,
Beispiel: x0=0,929683/2+1,25/2=1,089841; rel. Fehler=2,5*10-2; - eine Gerade mit optimierter Steigung und einer additiven Konstante (hier nicht näher betrachtet).
- eine einfache Konstante (beispielsweise 1),
- Ausgehend von dem so ermittelten Startwert x0 führt man eine feste Anzahl von Iterationsschritten durch. Die nötige Anzahl, um die gewünschte Genauigkeit zu erreichen, lässt sich dank der obigen Fehlerabschätzung als Worst Case innerhalb des Startintervalls direkt ausrechnen. Bei 32 Bits Mantisse und dem mittleren Startansatz braucht man beispielsweise nur drei Schritte. Diese fest gewählte Anzahl erspart wesentlich aufwendigere Abfragen auf Erreichung der Genauigkeit. Der Ersatz der genannten Konstanten durch die Zahl 1,0 ändert daran nichts. Auch der noch kompliziertere Ansatz brächte zumindest bei dieser Genauigkeit keine Einsparung eines weiteren Iterationsschritts. Bei höheren Genauigkeitsanforderungen kann das anders aussehen.
Beispiel mit drei Schritten nach Ansatz 1 (Konstante 1, mit den anderen Ansätzen konvergiert es noch einen Schritt schneller):
x1=(x0+a/x0)/2=(1+1,25/1)/2=1,125; rel. Fehler=6,2*10-3
x2=(x1+a/x1)/2=(1,125+1,25/1,125)/2=1,118056; rel. Fehler=2,0*10-5
x3=(x2+a/x2)/2=(1,118056+1,25/1,118056)/2=1,118034; rel. Fehler=0
Man sieht die Wirkung der quadratischen Konvergenz, dass sich der Fehler von Schritt zu Schritt jeweils quadriert oder die Anzahl gültiger Stellen bzw. der negative Fehlerexponent grob verdoppelt. - Zum Schluss wird der Exponent restauriert, indem man die Hälfte des im ersten Schritt abgespalteten Werts wieder hinzufügt.
Beispiel: x =2 * x3 = 2,236068 .
Verallgemeinerung des Verfahrens
Dieses Verfahren lässt sich verallgemeinern, so dass die k-te Wurzel von a berechnet wird. Je größer k ist, desto mehr Schritte werden benötigt, um die Wurzel genau zu berechnen.
Dazu wird die k-dimensionale Entsprechung der oben genannten geometrischen Herleitung benutzt.
Hier muss die Folge mit einem geeigneten Startwert für die Wurzel x0 gestartet werden.
Historisches
Die oben angegebenen Verfahren wurden zwar nach Heron von Alexandria benannt, verwenden aber eine Iteration von Dezimalzahlen, die Heron nicht kannte. Heron selbst verwandte in seiner Metrica zur Wurzelberechnung die Babylonische Wurzel-Methode
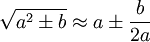 .
.
Diese Methode war bereits im altbabylonischen Reich bekannt, wo man mit Sexagesimalzahlen rechnete.[1]
Dazu zwei Beispiele:
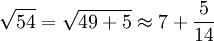 . Heron gibt hier den Wert
. Heron gibt hier den Wert 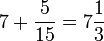 .
.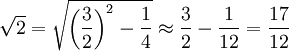 . Heron liefert hier ebenfalls den Wert
. Heron liefert hier ebenfalls den Wert 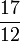 , der auch die grobe babylonische Näherung von
, der auch die grobe babylonische Näherung von 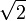 ist.
ist.Einzelnachweise
- ↑ Kurt Vogel: Vorgriechische Mathematik. Teil II: Die Mathematik der Babylonier, Hannover und Paderborn 1959, S. 34f.
Wikimedia Foundation.

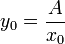

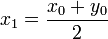
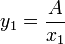


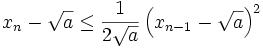 (
(