- Hölderstetigkeit
-
Die Hölder-Stetigkeit (nach Otto Hölder) ist ein Konzept der Mathematik, das vor allem in der Theorie der partiellen Differentialgleichungen von zentraler Bedeutung ist. Sie ist eine Verallgemeinerung der Lipschitz-Stetigkeit.
Inhaltsverzeichnis
Definition
Sei
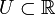 offen und
offen und 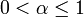 . Eine Abbildung
. Eine Abbildung 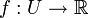 heißt hölderstetig zum Exponenten α genau dann, wenn eine positive reelle Zahl C existiert, so dass für alle
heißt hölderstetig zum Exponenten α genau dann, wenn eine positive reelle Zahl C existiert, so dass für alle 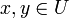 gilt:
gilt: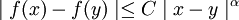 .
.
Eine Verallgemeinerung auf metrische Räume ist in natürlicher Weise gegeben.
Eigenschaften hölderstetiger Funktionen
Für α = 1 ergibt sich die Lipschitz-Stetigkeit. Jede hölderstetige Funktion ist gleichmäßig stetig: Setze für gegebenes
 etwa
etwa 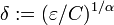 . Dann folgt aus
. Dann folgt aus 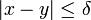 wie gewünscht
wie gewünscht 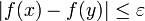 . Die Umkehrung gilt nicht, wie folgendes Beispiel zeigt:
. Die Umkehrung gilt nicht, wie folgendes Beispiel zeigt:Sei
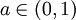 eine beliebig gewählte Konstante. Die auf dem Intervall [0,a] gemäß
eine beliebig gewählte Konstante. Die auf dem Intervall [0,a] gemäßdefinierte Funktion f ist laut Satz von Heine gleichmäßig stetig. Wäre sie auch hölderstetig, dann gäbe es Konstanten C > 0 und
![\alpha\in(0,1]](/pictures/dewiki/97/a20ad44a15374ffd41728fbd75899830.png) mit
mit 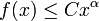 für alle
für alle ![x\in(0,a]](/pictures/dewiki/56/8b4c0c8714b535c14aaffe9d677dd102.png) , also insbesondere
, also insbesonderelaut Regel von L’Hospital, was einen Widerspruch ergibt.
Hölder-Raum
Ist
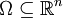 offen und beschränkt, so ist
offen und beschränkt, so istmit der Norm
ein Banachraum, der Hölder-Raum. Dabei sind die Laufvariablen β als Multiindizes zu verstehen. In der ersten Summe wird über die Supremumsnormen, in der zweiten über die so genannten Hölder-Halbnormen summiert.
Literatur
- H.W. Alt: Lineare Funktionalanalysis. Springer-Verlag, 2002
Wikimedia Foundation.

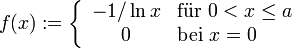
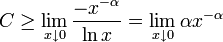
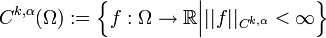
![\|f\|_{C^{k,\alpha}}:=\sum_{|\beta|\leq k}\underbrace{\sup_{x\in\overline{\Omega}}{\|D^\beta f(x)\|}}_{=:\, ||D^\beta f(x)||_{C(\Omega)}}+\sum_{|\beta|= k}\underbrace{\sup_{x\neq y}{\frac{|D^\beta f(x)-D^\beta f(y)|}{|x-y|^\alpha}}}_{=:\,[D^\beta f]_{C^{0,\alpha}(\Omega)}}](/pictures/dewiki/49/1d7412dbf1c9b2f492b9162794919ee1.png)