Idempotenzgesetz

Idempotenz ist ein Begriff aus der Mathematik und Informatik.

Er bezeichnet die Eigenschaft einer Funktion, in Verknüpfung mit sich selbst das gleiche Ergebnis zu liefern wie bei einmaliger Verwendung. Die beiden grundlegenden und wichtigsten Definitionen lauten:

Bei Funktionen oder unären Operationen bezeichnet man eine Funktion genau dann als idempotent, wenn gilt

f(x) = f(f(x)),

dass mehrmalige Anwenden einer Funktion also äquivalent mit der einmaligen Anwendung ist. Dafür kann man auch schreiben:

$f = (f\circ f)$.

Bei einer binären Operation bezeichnet man die Elemente, welche mit sich selbst verknüpft wieder sich selbst ergeben, also

$x \, \mbox{Op} \, x = x$,

als idempotente Elemente.

Beispiele für idempotente Funktionen

• Konstante Funktion: f(x) = c.
• Identität: f(x) = x.
• Projektionen, z.B. p(x,y) = (x,0)
• Betrag einer reellen oder komplexen Zahl: f(x) = | x | .
• Hüllenfunktionen

Beispiele für idempotente Elemente bei binären Verknüpfungen

• Bei der Multiplikation auf den reellen Zahlen sind 0 und 1 die beiden einzigen idempotenten Elemente (da 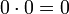$0 \cdot 0 = 0$ und $1 \cdot 1 = 1$).
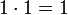• Beim Logischen Und sind sowohl Wahr als auch Falsch idempotent.
• Beim Logischen Oder sind sowohl Wahr als auch Falsch idempotent.
• Unter der Vereinigung und dem Durchschnitt in der Mengenlehre sind alle Mengen idempotent.

Idempotente Matrizen

Eine quadratische Matrix A der Dimension n über einem beliebigen Körper K heißt idempotent genau dann, wenn die durch sie induzierte lineare Abbildung

$f: K^n \to K^n,$

$v \mapsto Av$

idempotent gemäß obiger Definition ist. Dies ist genau dann der Fall, wenn A² = A gilt. Insbesondere sind die Eigenwerte von A allesamt 0 oder 1. Geometrisch können idempotente lineare Abbildungen als Projektion des Vektorraums auf einen Untervektorraum interpretiert werden.

Siehe auch: Nilpotenz, Involution

Informatik

In der Informatik wird Idempotenz von Recovery-Maßnahmen bei Datenbanken gefordert, um Fehlertoleranz bei einem Absturz während einer Wiederanlaufphase zu gewährleisten. Undo- und Redo-Operationen müssen hier auch bei mehrfacher Hintereinanderausführung dasselbe Resultat zur Folge haben.