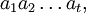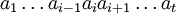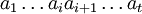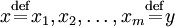- Amalgamierte Untergruppe
-
Das amalgamierte (freie) Produkt von Gruppen Gi nach der Gruppe U oder das freie Produkt der Gruppen Gi mit der amalgamierten Untergruppe U ist eine mit dem freien Produkt von Gruppen verwandte mathematische Konstruktion. Dabei wird zum Einen das freie Produkt der Gruppen gebildet, die allerdings alle eine zur (Unter-)Gruppe U isomorphe Untergruppe enthalten müssen. Zum Anderen werden diese Untergruppen durch geeignete Identifikation von Elementen und Anpassung der Gruppenverknüpfung dann innerhalb des freien Produktes bildlich gesprochen miteinander verschmolzen und in diesem Sinne amalgamiert[1]. Die Identifizierung von je zwei Elementen aus verschiedenen Untergruppen wird hierbei über die Isomorphie zur Gruppe U bewerkstellig (s. u. Ä3) und dementsprechend die Gruppenverknüpfung angepasst (s. u. Gruppen-Verknüpfung).
Das freie Produkt ist eine Anwendung bzw. ein Spezialfall des amalgamierten Produktes, da jedes freie Produkt vermöge der Amalgamierung nach der trivialen Untergruppe {1}[2] einer seiner Faktoren als amalgamiertes Produkt aufgefasst werden kann.
Inhaltsverzeichnis
Definition (konstruktiv)
Grundvoraussetzungen
Sei
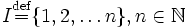 eine Indexmenge und
eine Indexmenge und 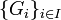 eine Familie von Gruppen. Weiter beinhalte jede dieser Gruppen eine Untergruppe Ui und alle diese Ui seien isomorph zu einer einzelnen weiteren Gruppe U. (Der zugehörige Gruppen-Isomorphismus, welcher diese Isomorphie vermittelt, sei mit
eine Familie von Gruppen. Weiter beinhalte jede dieser Gruppen eine Untergruppe Ui und alle diese Ui seien isomorph zu einer einzelnen weiteren Gruppe U. (Der zugehörige Gruppen-Isomorphismus, welcher diese Isomorphie vermittelt, sei mit 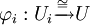 für alle
für alle 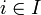 bezeichnet.)
bezeichnet.)Sei weiter
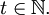 Ein Wort über den Gi sei eine Hintereinanderschreibung (Aneinanderreihung, Verkettung, etc.)
Ein Wort über den Gi sei eine Hintereinanderschreibung (Aneinanderreihung, Verkettung, etc.)wobei das Wort entweder (für t = 0) leer sei – dann geschrieben 1 oder ε – oder es gelte
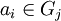 für ein
für ein 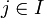 , für jedes
, für jedes 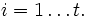 (D. h. zwei verschiedene ai müssen nicht aus derselben Gruppe sein!)
(D. h. zwei verschiedene ai müssen nicht aus derselben Gruppe sein!)(Im Folgenden schreiben wir sowohl für das leere Wort wie auch für die neutralen Elemente 1j der Gruppen Gj ohne Unterschied 1.)
Äquivalenzrelation
Elementare Äquivalenzen
Analog zum Vorgehen bei der Bildung des freien Produktes der Gruppen Gi betrachten wir nun Wörter aus Elementen aus den Gi und definieren sogenannten elementare Äquivalenzen (Ä1–Ä3) zwischen denselben:
(Ä1)
- – Neutrale Elemente können weggelassen werden. –
- Falls ai = 1, dann sei
- (elementar) äquivalent zu
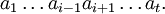
(Ä2)
- – Zwei Elemente können durch ihr Produkt ersetzt werden. –
- Falls ai und ai + 1 aus derselben Gruppe Gj sind und aiai + 1 = a * in Gj gilt, dann sei
- (elementar) äquivalent zu
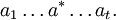
(Ä3)
-
- Zwischenbemerkung:
- Wir sagen, zwei Elemente
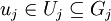 und
und 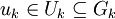 mit
mit 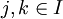 seien einander zugehörig, falls sie, vermittels der Isomorphismen
seien einander zugehörig, falls sie, vermittels der Isomorphismen 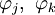 zwischen Uj, Uk und U, demselben
zwischen Uj, Uk und U, demselben 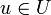 entsprechen; d. h. falls
entsprechen; d. h. falls 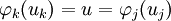 gilt.
gilt.
- Zwischenbemerkung:
- – Elemente können durch zugehörige Elemente ersetzt werden. –
- Falls
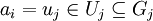 und
und 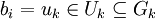 mit
mit 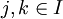 und die Elemente uj und uk einander zugehörig sind, dann sei
und die Elemente uj und uk einander zugehörig sind, dann sei
- (elementar) äquivalent zu
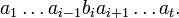
Wortweise Äquivalenz
Auf Grundlage der elementaren Äquivalenzen Ä1–Ä3 erklären wir nun die wortweise Äquivalenz: Zwei Wörter x und y sind (wortweise) äquivalent, falls es eine Folge
mit
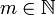 gibt, in welcher xi und xi + 1 für jedes
gibt, in welcher xi und xi + 1 für jedes 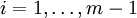 elementar äquivalent sind. (Die wortweise Äquivalenz entspricht damit der transitiven Hülle bzw. der reflexiv-transitiven Hülle der elementaren Äquivalenz.)
elementar äquivalent sind. (Die wortweise Äquivalenz entspricht damit der transitiven Hülle bzw. der reflexiv-transitiven Hülle der elementaren Äquivalenz.)Gruppen-Verknüpfung
Auf der Quotientenmenge nach der so definierten Äquivalenzrelation definieren wir endlich noch kanonisch die Gruppen-Verknüpfung:
![[x][y] \stackrel{\mathrm{def}}= [xy]](/pictures/dewiki/55/71fbba1041d2191a156611855c5d2acc.png) (kanonisches Produkt).
(kanonisches Produkt).
Abschlussdefinition
Die Quotientenmenge bildet zusammen mit dem eben definierten Produkt eine Gruppe, nämlich das amalgamierte Produkt der Gruppen Gi oder das freie Produkt der Gruppen Gi mit der amalgamierten Untergruppe U.
Weblinks
Quellen
- Hall, Marshall: The theory of groups. Macmillan, New York, 1959.
Fußnoten / Einzelnachweise
- ↑ Vgl. dazu den entsprechenden Wiktionary-Eintrag unter Weblinks.
- ↑ Die Untergruppen
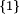 sind trivialerweise alle isomorph zur jeder beliebigen Gruppe der Gruppenordnung 1. Man wähle
sind trivialerweise alle isomorph zur jeder beliebigen Gruppe der Gruppenordnung 1. Man wähle 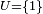 als Amalgamierungsuntergruppe.
als Amalgamierungsuntergruppe. - ↑ Die Folge ist
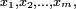 wobei
wobei 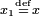 und
und 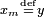 gesetzt wird. – „Bei der Interpretation der Formel werden Gleichheitszeichen vor Kommata ausgewertet.“
gesetzt wird. – „Bei der Interpretation der Formel werden Gleichheitszeichen vor Kommata ausgewertet.“
Wikimedia Foundation.