Inversor von Peaucellier

Der Inversor von Peaucellier ist ein Koppelgetriebe zur Überführung einer Kreisbewegung in eine Geradenbewegung und umgekehrt. Benannt ist er nach Charles-Nicolas Peaucellier, der ihn 1864 erfand. Bis zur Erfindung dieses Mechanismus kannte man keine planare Methode, geradlinige Bewegungen zu erzeugen, ohne Linearführungen wie etwa Schienenführungen zu verwenden. Anwendung fand der Inversor z.B. beim Bau von Kolbendampfmaschinen.

• 

  Animation zur Funktionsweise des Inversors

• 

  Die geometrische Grundlage des Inversors

Funktionsweise

Der Inversor von Peaucellier beruht auf der Inversion am Kreis, die die Eigenschaft besitzt, Kreise durch den Inversionsmittelpunkt in Geraden zu überführen. Auf Grund dieser Eigenschaft kann der Inversor von Peaucellier auch zur Konstruktion eines Bildpunktes unter der Inversion verwendet werden.

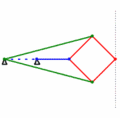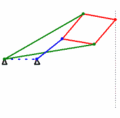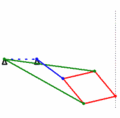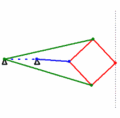
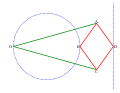
Der Inversor besteht aus zwei langen Stangen (grün, jeweils mit der Länge a) und vier kürzeren (rot, jeweils mit der Länge b), die mit Gelenken verbunden sind. Auf Grund seiner Konstruktion sind die Gelenke B und D invers zueinander, wobei der Inversionskreis seinen Mittelpunkt in O mit einem Radius von $\sqrt{a^2-b^2}$ hat. Bewegt sich also B auf einem Kreis durch O (in der Animation wird dies durch die blaue Stange realisiert), so bewegt sich der Punkt D auf einer Geraden.

In der Praxis kann sich das Gelenk B nur auf einem Teil des Kreises bewegen, da er durch den Mechanismus dem Punkt O nicht beliebig nahe kommen kann. Ein weiteres Problem in der Praxis stellen die vielen Gelenke dar.

Literatur

• Coxeter, H. S. M., und S. L. Greitzer: Zeitlose Geometrie, Klett Stuttgart 1983, ISBN 3129833900

Weblinks

• Peaucellier Apparatus (engl.)