- Wattgestänge
-
Inhaltsverzeichnis
Ursprung
Das Wattsche Parallelogramm ist ein Maschinenelement zur Umwandlung einer rotatorischen Schwenkbewegung in eine annähernd geradlinige Bewegung. Erfunden wurde es von James Watt im Jahre 1784, der es erstmals an der von ihm weiterentwickelten Dampfmaschine verwendete.
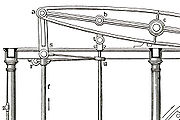
Das Wattsche Parallelogramm diente in diesem Fall zur Verbindung der Kolbenstange der Maschine mit dem um einen festen Drehpunkt hin- und herschwingenden Balancier, dem zentralen Hebel der frühen Bauarten der stehenden Dampfmaschine. Es besteht aus einzelnen Kuppelstangen, in die zur Verbindung mit den Nachbarstäben jeweils ein Bolzen eingeschoben ist.
Wirkungsweise
Das Wattsche Parallelogramm besteht aus zwei Komponenten, dem Wattgestänge und dem eigentlichen Parallelogramm.
Das Wattgestänge
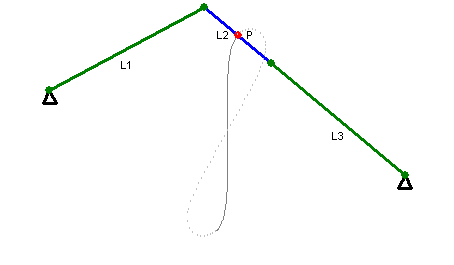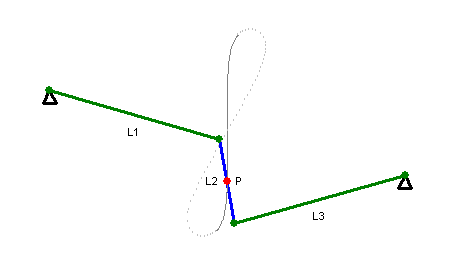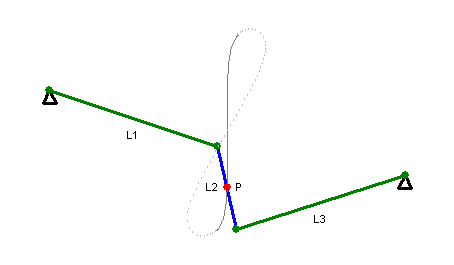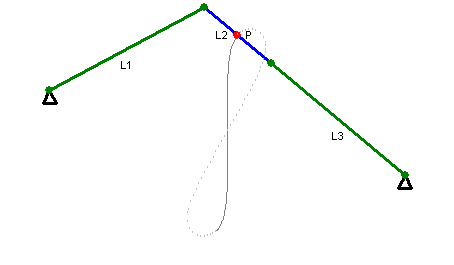
Das Wattgestänge (in manchen Einsatzbereichen auch als Lemniskatenlenker bezeichnet) ist der eigentliche Mechanismus, der die Bewegung eines Punktes auf einem Kreisbahnabschnitt in eine Bewegung auf einer Lemniskate umsetzt. Im nutzbaren Bereich des Wattgestänges ist die Lemniskate annähernd eine Gerade.
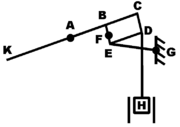
Im linken Diagramm besteht das Wattgestänge nur aus den beiden festen Punkte A und G, den beiden Hebeln AB und EG, die sich in A und G drehen können, und dem Hebel BE, der an seinen Endpunkten drehbar(!) mit den beiden genannten Hebeln verbunden ist. Wenn der Hebel AB hin- und hergedreht wird, bewegt sich Punkt F auf einer beinahe geraden Linie auf und ab.
Das rechte Diagramm zeigt den Bewegungsablauf eines Wattgestänges ohne das Parallelogramm. Hier bewegen sich die Endpunkte von L1 und L3 auf Kreisbahnen, der Punkt P auf einer Lemniskate.
Andere mechanische Konstruktionen, die eine rotatorische Schwenkbewegung in eine geradlinige Bewegung umsetzen, sind der Inversor von Peaucellier und das Tschebyschow-Parallelogramm.
Das Parallelogramm
Das Parallelogramm wird im linken Diagramm von den Punkten BCDE gebildet, wobei alle vier Eckpunkte drehbare Gelenke sind. Es hat die Funktion eines Pantografen - da die Punkte A, F und D bei passender Länge von CD auf einer Geraden liegen und der Abstand von A zu D immer proportional dem Abstand von A zu F ist, vollführt also D die gleiche Bewegung wie F, nur „vergrößert“. Wenn sich F auf einer (beinahe) geraden Linie bewegt, dann also auch D - der Punkt, der mit dem Kolben H verbunden ist.
Zum Betrieb einer Maschine wäre das Parallelogramm streng genommen nicht nötig - man könnte die Stange, die am Kolben H beginnt, auch direkt mit F verbinden. Das hätte aber zur Folge, dass der Kolbenhub sehr viel geringer wäre oder, um den gleichen Hub zu erzielen, die Punkte B, E und vor allem G sehr viel weiter nacht rechts wandern müssten, was den Platzbedarf der Maschine deutlich vergrößern würde.
Das Umsetzung der Bewegung durch das Wattgestänge und die Vergrößerung des Hubs durch ein Parallelogramm sind zwei also unabhängige Mechanismen, die auch separat verwendet werden können.
Würdigung
Die Erfindung wirkte sehr schnell über die Technologie der Dampfmaschine hinaus, denn die Wandlung von Bewegungsarten hat ganz zentrale Bedeutung. So hat zum Beispiel die Achsschenkellenkung, die in jedem modernen Kraftfahrzeug einen wesentlichen Teil der Lenkung darstellt, ihren Ursprung im Wattschen Parallelogramm.
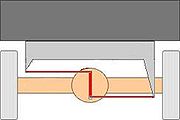
Das Wattgestänge (ohne das Parallelogramm) wird an manchen Autos mit Starrachse eingesetzt, um eine Seitwärtsbewegung der Achse zu verhindern. Die Vertikalbewegung der Achse entspricht damit sehr viel besser einer geraden Linie als z.B. bei Verwendung eines Panhardstabs.
Unter dem Namen „Lemniskatenlenker“ wird das Wattgestänge bei Schienenfahrzeugen eingesetzt, um eine Bewegung der Radachsen in Längsrichtung des Zuges zu verhindern.
James Watt schrieb über seine Erfindung: „Obwohl ich um Ruhm mich nicht sorge, bin ich doch auf die Parallelbewegung stolzer als auf irgendeine Erfindung, die ich gemacht habe.“
Weblinks
Eine Animation der Lemniskate zur Erläuterung der Funktion des Wattschen Parallelogrames (Java-Applet)
Zur Erläuterung: Der Punkt E lässt sich mit dem Mauszeiger anfassen und um den Mittelpunkt A des blau gezeichneten Kreises drehen. Der hier interessierende Teil der Lemniskate ergibt sich dann aus den geraden Abschnitten der 8-förmigen Kurve.
Wikimedia Foundation.