Irrlauf

Zufallsbewegungen bzw. Irrfahrten (englisch random walk) bilden eine wichtige Klasse stochastischer Prozesse. Sie dienen der Modellierung nichtdeterministischer Zeitreihen und der Herleitung von Wahrscheinlichkeitsverteilungen.

Simulation mehrerer 1D Random Walks.

Der eindimensionale Random Walk dient als verallgemeinerungsfähiges Einführungsbeispiel, hat aber auch eigenständige Anwendungen.

Der eindimensionale Random Walk ist ein Bernoulli-Prozess, das heißt eine Folge von unabhängigen Bernoulli-Versuchen; er führt zu einer Binomialverteilung.

Eine beliebte Veranschaulichung lautet ungefähr wie folgt: Ein desorientierter Fußgänger läuft in einer Gasse mit einer Wahrscheinlichkeit p einen Schritt nach vorne, mit einer Wahrscheinlichkeit q = 1 − p einen Schritt zurück. Wie groß ist die Wahrscheinlichkeit, dass er nach n Schritten eine Strecke X zurückgelegt hat? Antwort:

$P(X=-n+2k) = { n \choose k } ~ p^k q^{n-k}$.

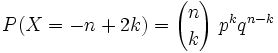Die Abbildung oben zeigt 5 Simulationen für n=300 Schritte mit einer variablen Schrittlänge von -0,5 bis 0,5 Einheiten. Da die Schritte durch gleichverteilte Zufallszahlen simuliert werden, beträgt die mittlere Schrittlänge 0,25. Die Varianz E(X²) beträgt n. Die Standardabweichung der Entfernung vom Ursprung ist 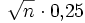$\sqrt{n}\cdot 0{,}25$ Schritte. Sie ist als rote Linie für positive und negative Entfernungen eingezeichnet. Um diese Strecke wird sich der Fußgänger fortbewegen. Die relative Abweichung 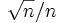$\sqrt{n}/n$ geht gegen null, aber die absolute Abweichung 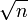$\sqrt{n}$ wächst unbeschränkt.

Simulation eines 2D-Random Walk mit 229 Schritten und einer zufälligen Schrittweite aus dem Intervall [-0,5;0,5] für x- und y-Richtung.

Oft interessiert man sich speziell für den ungerichteten Random Walk mit p=q=1/2. Dann ist die Wahrscheinlichkeitsverteilung der zurückgelegten Strecke symmetrisch um X=0, und auch der Erwartungswert ist E(X)=0. Das Vorankommen des Fußgängers kann man dann nur durch den mittleren quadratischen Abstand vom Ausgangspunkt, also die Varianz der Binomialverteilung beschreiben: E(X²) = n. Das ist ein nichttriviales Ergebnis, mit dem eine charakteristische Eigenschaft von Diffusionsprozessen und Brownscher Molekularbewegung wiedergefunden wird: das mittlere Quadrat des Abstands eines diffundierenden Teilchens von seinem Ausgangsort wächst proportional zur Zeit.

Siehe auch

• Zufallspfad
• Wiener-Prozess
• Random-Walk-Theorie
• Freely-Jointed-Chain-Modell