Jakobsstab

Winkelmessung mit dem Jakobstab, aus Introductio geographica des Peter Apian, 1523

Ein Jakobsstab (lateinisch baculus jacobi), auch Gradstock oder Kreuzstab, ist ein früheres astronomisches Instrument zur Winkelmessung und zur mittelbaren Streckenmessung. Es wurde vor allem in der Seefahrt, aber auch in der Landvermessung und Astronomie verwendet. Der Name kommt von einer gewissen Ähnlichkeit mit dem ebenfalls als „Jakobsstab“ bezeichneten Pilgerstab der Jakobspilger. Der Jakobsstab war in der Nautik der Vorläufer des Sextanten.

Die Erfindung des Jakobsstabs liegt zwar im 13. Jahrhundert, aber erst Johannes Müller, genannt Regiomontanus, machte das Instrument im 15. Jahrhundert zu einem beliebten Messgerät.^[1]

Das Gerät diente in der Seefahrt hauptsächlich der Bestimmung der geographischen Breite. Dazu wurde der Höhenwinkel der Sonne oder eines Fixsternes (meist des Polarsterns) über dem nautischen Horizont gemessen. Bei der küstennahen Navigation wurden mit ihm auch Winkel zwischen terrestrischen Zielen gemessen und damit in der Karte die Position bestimmt.

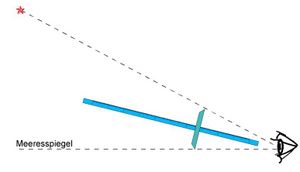
Der Jakobsstab besteht aus einem Basisstab mit Ableseskala und mehreren Querhölzern, von denen für eine Messung ein oder zwei verwendet werden, deren Auswahl sich nach dem benötigten Winkelbereich richtet. Die Querhölzer verleihen ihm ein armbrustähnliches Aussehen, weswegen bis heute bei Verwendung des Sextanten gesagt wird, man schießt einen Stern, wenn man seine Höhe über dem Horizont misst.

Man verwendet ihn, indem man den Längsstab am Jochbein unter dem Auge ansetzt und anschließend das Querstück so lange verschiebt, bis dessen Enden den Horizont und den angepeilten Stern gerade überdecken. Die halbe Länge des Querstabes, dividiert durch die am Hauptstab abgelesene Länge (Abstand vom Auge zum Querstab), ergibt den Tangens des halben gesuchten Winkels zwischen Horizont und Stern. Die Skalierung des Querstabes war häufig so ausgeführt, dass für eine bestimmte Querstab-Länge der Winkel direkt abgelesen werden konnte.

Zur Entfernungsmessung wird der Winkel α einer Basis mit bekannter Länge gemessen. Dazu eignet sich zum Beispiel ein Turm bekannter Höhe h. Der Abstand a zum Turm ergibt sich für große Entfernungen in guter Näherung, bei lotrechtem Querstab auch genau, aus

$s = \frac{b}{2} \cdot \cot \frac{\alpha}{2}$

Die Anwendung ist schwierig, da während des Verschiebens des Querstabs über die Skala gleichzeitig die beiden Peilungen aufrechterhalten werden müssen, was besonders auf einem schwankenden Schiff kaum mit der wünschenswerten Genauigkeit durchzuführen ist.

Benutzung des Jakobsstabes zur Bestimmung der Höhe eines Gegenstandes

Anwendung: Bestimmung des Höhenwinkels eines Sterns über dem Meeresspiegel

Um die Höhe eines beliebigen Gegenstandes zu bestimmen, muss man die Entfernung zu ihm kennen. Der Mathematiker Philipp Apian (1531-1589) beschrieb eine Methode, mit dem Jakobsstab die Höhe des Gegenstandes zu bestimmen. Nach ihm müsse man den Jakobsstab so an das Auge halten, dass das obere Ende des Läufers am oberen Ende des Gegenstandes zu sehen ist und das Untere entsprechend am unteren Ende des Gegenstands. Dann berechnet man nach Apian die Höhe h des Gegenstands mit folgender Formel:

a = die Entfernung zum Gegenstand

l = die Länge des Läufers

b = die Entfernung vom Auge bis zum Läufer.

$h= \frac {a \cdot l} {b}$

Bei dieser Rechnung benutzt Apian den 2. Strahlensatz. Die Bedingungen für diesen Satz sind hier jedoch nicht immer erfüllt, denn der Läufer ist nicht unbedingt parallel zum Gegenstand. Auf große Entfernungen wirkt sich dieser Fehler jedoch nur gering aus. Zur genauen Bestimmung der Höhe gibt es zwei Möglichkeiten. Die erste ist die einfachere, bei der keine Winkelfunktionen benötigt werden. Dabei muss man den Jakobsstab so halten, dass der Läufer parallel zum Gegenstand ist und man das obere Ende des Läufers wieder am oberen Ende des Gegenstandes sieht. Dann lautet die Formel zur Berechnung der Höhe h:

h_b = die Augenhöhe

b = die Entfernung zum Gegenstand

l = die Länge des Läufers

d = die Entfernung vom Auge bis zum Läufer.

$h=h_b + \frac {b \cdot l} {2d}$

Die zweite Methode ist etwas komplizierter, da Winkelfunktionen benutzt werden. Der Jakobsstab muss wieder gehalten werden, wie es Apian beschrieb. Auch hier wird die Augenhöhe h_a benötigt.

s_G = die Entfernung zum Gegenstand

h_s = die Länge des Läufers

l_s = die Entfernung des Läufers zum Auge

h_G = die Höhe des Gegenstands

Die Formel lautet:

$h_G=\tan (\cos^{-1} (\frac {h_a} {\sqrt{h_a^2+s_G^2}})+2 \cdot \cos^{-1}(\frac {l_s} {\sqrt{(\frac {h_s} {2})^2+l_s^2}})-90^\circ)\cdot s_G+h_a$

Der Vorteil der zweiten Methode ist, dass man nicht darauf achten muss, ob der Läufer parallel zum Gegenstand ist und der Jakobsstab somit parallel zum Boden ist. Dafür ist diese Formel schwer auswendig zu lernen.

Siehe auch

• Bussole – Teilkompass zur präzisen Ausrichtung mit Hilfe einer langen Magnetnadel
• Spiegelsextant – heutiges Gerät für astronomische Navigation
• Theodolit – Instrument zur Landvermessung (Geodäsie)
• Peilung
• Faustregel
• Daumenregel
• Daumensprung
• Stockpeilung

Einzelnachweise

1. ↑ Ralf Kern: Wissenschaftliche Instrumente in ihrer Zeit. Vom Astrolab zum mathematischen Besteck. Köln: Verlag der Buchhandlung Walther König, 2010. S. 214.

Literatur

• Franz Adrian Dreier: Winkelmeßinstrumente. Vom 16. bis zum frühen 19. Jahrhundert. Kunstgewerbemuseum, Berlin 1979 (Ausstellungskatalog, Berlin, Kunstgewerbemuseum, 9. November 1979 – 23. Februar 1980).
• Willem F. J. Mörzer Bruyns: The Cross-Staff. History and Development of a Navigational Instrument. Vereeniging Nederlandsch Historisch Scheepvaart Museum, Zutphen 1994, ISBN 90-6011-907-X (Vereeniging Nederlandsch Historisch Scheepvaart Museum. Jaarboek 1994).
• Albert Schück: Der Jakobsstab. In: Jahresbericht der Geographischen Gesellschaft München. Heft 2, 1894/1895, ISSN 0938-2097, S. 93–174.

Weblinks

 Commons: Jacob's staff – Sammlung von Bildern, Videos und Audiodateien

• Informationsseite und Beschreibung des Jakobstabes
• Informationsseite der TU Freiberg
• Informationsseite des Schiffahrtsmuseums der Oldenburgischen Weserhäfen Archiv-Version