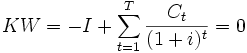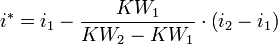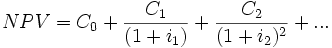Kapitalertragsrate

Die Interne-Zinsfuß-Methode (auch Interne-Zinssatz-Methode; engl.: IRR, Internal Rate of Return), ist ein Verfahren der dynamischen Investitionsrechnung. Der Abzinsungsfaktor, bei dessen Verwendung die diskontierten künftigen Zahlungen dem heutigen Preis entsprechen, heißt interner Zinsfuß. Ist dieser Zinsfuß größer als der Kalkulationszinsfuß, ist die Investition wirtschaftlich.

Vorgehen

Es wird derjenige Zinssatz i gesucht, bei dem der Kapitalwert

• $KW = -I+\sum_{t=1}^T \frac{C_t}{(1+i)^t}=0$

(oder Net Present Value (NPV)) des gegebenen Projektes gleich Null ist. Dabei wird die Investition I der Summe aller abgezinsten Cash-Flows (Zahlungen) C_t zu Zeitpunkten t gegenübergestellt.

Zur Lösung der Gleichung, d. h. zur Bestimmung des Zinsfußes i, bedient man sich zumeist eines Interpolationsverfahrens:

1. Man wähle einen ersten geschätzten Zinsfuß i₁ und berechne damit den Kapitalwert KW₁ des Investitionsobjektes
2. Ist KW₁ > 0 ( KW₁ < 0 ), so wähle man einen Zinsfuß i₂ > i₁ ( i₂ < i₁ ) und berechne damit KW₂
3. Aus den Werten i₁, i₂ und KW₁, KW₂ bestimme man durch Interpolation den Näherungswert i ^* für den tatsächlichen Zinsfuß i.

Geeignet ist die folgende Interpolationsformel:

• $i^*=i_1 - \frac{KW_1}{KW_2 - KW_1} \cdot \left( i_2 - i_1 \right)$

Bezüglich der Versuchszinssätze (i₁,i₂) sollte erwähnt werden, dass bei Finanzinvestitionen nur eine Differenz von bis zu 0,5 % sinnvoll ist. Bei Sachinvestitionen sind dagegen größere Differenzen möglich (bis zu 5 %). Allgemein gilt: Je näher die Versuchszinssätze zusammenliegen, umso kleiner ist der Interpolationsfehler.

In der Praxis wird ein mathematisches Lösungsverfahren für geometrische Reihen wie das Newton-Verfahren oder Regula Falsi verwendet. Moderne Tabellenkalkulationsprogramme wie beispielsweise MS Excel enthalten Add-ons, welche die Nullstellenberechnung unterstützen (Solver, auf Deutsch Zielwertsuche).

Problematisch ist jedoch, dass geometrische Reihen mit häufigen Vorzeichenwechseln dazu führen, dass rechnerisch möglicherweise mehrere Nullstellen existieren. Derartige Reihen müssen erst bereinigt werden. Hierfür kann ein Startwert für den Zinssatz angegeben werden.

Kritische Einschätzung

Kreditgewährung oder Kreditaufnahme

Werden die folgenden beiden Projekte miteinander verglichen, hilft die Interne-Zinsfuß-Methode nicht weiter:

Projekt	C0	C1	IZF	NPV bei 10%
A	-2.000	+3.000	+50%	+727
B	+2.000	-3.000	+50%	-727

Beide Projekte weisen den gleichen internen Zinsfuß auf (-2.000 + 3.000/1,50 = 0 und +2.000 - 3.000/1,50 = 0), sind nach dieser Methode also gleich attraktiv. Allerdings wird bei Betrachtung des NPV (oder in diesem Fall: dem genauen Hinsehen) klar, dass bei Projekt A initial Geld zu 50% verliehen wird und bei Projekt B geliehen wird. Wenn Geld geliehen wird, ist ein niedriger Zinssatz gewünscht, das heißt der IZF sollte niedriger sein als die Opportunitätskosten und nicht höher.

Mehrere Interne Zinsfüße

In den meisten Ländern werden die Steuern im Folgejahr gezahlt, das heißt, dass der Gewinn und die Steuerlast nicht in der gleichen Periode anfallen. Das folgende Beispiel ist ein Projekt, das eine Investition in Höhe von 2.000.000€ erfordert und dabei während seiner (hier fünfjährigen) Laufzeit einen zusätzlichen Profit in Höhe von 600.000€ p.a. einbringt. Der Steuersatz beträgt 50% und wird in der Folgeperiode gezahlt:

	C0	C1	C2	C3	C4	C5	C6
Cash Flow vor Steuern	-2.000	+600	+600	+600	+600	+600
Steuern		+1.000	-300	-300	-300	-300	-300
Netto Cash Flow	-2.000	+1.600	+300	+300	+300	+300	-300

(Anmerkung: Die Investition i.H.v. 2 Mio.€ in C₀ verringert die Steuerlast für diese Periode um 1.000.000€, die in C₁ hinzugefügt wird.)

Die Berechnungen des IZF und NPV ergeben folgendes:

IZF	NPV bei 10%
-50% und 15,2%	149,71 oder 149.710€

Bei beiden Zinssätzen ist die Bedingung NPV=0 erfüllt. Der Grund hierfür liegt in dem zweimaligen Vorzeichenwechsel in der Zahlungsreihe: Nach Descartes kann eine Polynomgleichung soviele mathematisch gültige Lösungen haben wie Vorzeichenwechsel. Im Beispiel führt dieser zweimalige Vorzeichenwechsel dazu, dass das (mathematisch richtige) Ergebnis nicht ökonomisch interpretierbar ist (Welcher interne Zinsfuß ist richtig?).

In der Praxis kommen solche Reihen nicht nur durch die Verzögerung der Steuerzahlungen zustande, sondern können auch durch Wartungskosten während der Laufzeit des Projektes oder die Verschrottung einer Anlage am Ende der Laufzeit entstehen.

Eine Möglichkeit in der Umgehung eines abschließenden (zweiten) Vorzeichenwechsels besteht darin, einen modifizierten IZF zu berechnen: Der Cash Flow im 6. Jahr wird im 5. berechnet und zu diesem hinzugefügt und der IZF erneut berechnet.

Sich gegenseitig ausschließende Projekte

Um einen bestimmten Auftrag zu erfüllen, haben Firmen oft die Wahl zwischen sich gegenseitig ausschließenden Projekten. Auch hier kann die IZF-Methode in die Irre führen:

Projekt	C0	C1	IZF	NPV bei 10%
C	-20.000	+40.000	+100%	+16.363
D	-40.000	+70.000	+75%	+23.636

Beide Projekte sind lukrativ und nach der IZF Entscheidungsregel müsste Projekt C durchgeführt werden, aber wie der NPV zeigt, ist D gegenüber C vorzuziehen, da es den höheren Geldwert hat. Dennoch kann die IZF-Methode auch hier zum Einsatz kommen: Bei Betrachtung der inkrementellen Zahlungsströme (die Differenz beider Projekte) führt der interne Zinsfuß zum gleichen Ergebnis wie die Kapitalwertmethode (der inkrementelle IZF ist 50%, das heißt, wenn der inkrementelle IZF größer ist als der Kalkulationszinsfuß, sollte das "größere" Projekt - hier Beispiel D - durchgeführt werden.).

Vernachlässigung der Zinsstruktur

Die IZF-Methode geht von der Annahme aus, dass die kurz- und langfristigen Zinssätze identisch sind (siehe Formel, nur ein Zinssatz). Dies trifft in der Realität selten zu und die Zinssätze unterscheiden sich in Bezug auf die Fristigkeit erheblich ("kurzes Geld", das heißt Kredite mit einer relativ kurzen Laufzeit weisen einen niedrigeren Zinssatz auf, sind also billiger, als "langes Geld", das heißt Kredite mit längerer Laufzeit. Inverse Zinsstrukturen sind beispielsweise Anfang der 1990er Jahre beobachtet worden.). Bei der Kapitalwertmethode stellt dies kein Problem dar, da einfach die Zahlungsströme mit unterschiedlichen Zinssätzen abgezinst werden können:

• $NPV = C_0+ \frac{C_1}{(1+i_1)}+ \frac{C_2}{(1+i_2)^2}+...$

Eine Alternative besteht darin, mit dem gewichteten Durchschnitt der Zinsen über die Laufzeit zu rechnen, jedoch wenden Kritiker dieser Variante ein, dass sie die Komplexität der Rechnung unnötig erhöht bei Vorliegen einer einfachen Lösung.

In der Praxis wird die Zinsstrukturproblematik, und damit die Frage mit welchem Zinssatz der IZF verglichen werden soll (i₁, i₂ oder i₅), meist vernachlässigt.

Fazit

• Die Methode des internen Zinsfußes ist nicht dazu geeignet, mehrere Investitionsprojekte unterschiedlicher Höhe, Dauer und Investitionszeitpunkte miteinander zu vergleichen. Es ist gut möglich, dass eine Investition mit einem höheren internen Zinsfuß einen geringeren Kapitalwert hat als eine andere Investition mit niedrigerem IZF.
• Weiterhin geht diese Methode davon aus, dass sämtliche Kapitalrückflüsse zum internen Zinssatz wieder angelegt werden (Wiederanlageprämisse) und nicht zum Marktzinssatz (Kapitalwertmethode). Die Wiederanlageprämisse wird in der Praxis überwiegend als unrealistisch eingeordnet.
• Die genannten Beispiele zeigen, dass es durchaus möglich ist, die IZF-Methode so zu modifizieren, dass sie brauchbare Ergebnisse liefert. Es stellt sich jedoch die Frage, ob dies nötig ist in Anbetracht der Zuverlässigkeit und mathematischen Einfachheit der Kapitalwertmethode.
• Die Methode des internen Zinssatzes eignet sich in der Praxis gut zur Beurteilung von Einzelinvestitionen in unvollständig definierten Szenarien. Maßgröße ist eine gewünschte Mindestrendite. Übersteigt der Zinssatz diese Mindestrendite, so ist die Investition für sich genommen sinnvoll.
• Die aufgezeigten Möglichkeiten, die Interne-Zinsfuß-Methode praktisch verwertbar zu machen, laufen im Ergebnis auf eine Anwendung der Kapitalwertmethode hinaus: Die konkrete Investition wird über Umwege (IZF-Methode) oder direkt (Kapitalwertmethode) mit einem Referenzzinssatz verglichen.

Varianten der internen Zinsfußmethode

Zur internen Zinsfußmethode ergeben sich in der Praxis verschiedene Varianten, je nach dem ob mit exponentiellen Verzinsung und linearer Verzinsung operiert wird. Dies ist im Folgenden dargestellt.

Praktische Varianten der Internen Zinsfuß-Methode
	ISMA	SIA	Treasury	Moosmüller
Umrechnung einer Periodenrendite auf eine Jahresrendite	exponentiell	unterjährig linear	unterjährig linear	exponentiell
Diskontierung der ersten vollständigen Kuponperiode	exponentiell	exponentiell	linear	linear
Berechnung der Rendite bei Restlaufzeiten unter einem Jahr	exponentiell	exponentiell	linear	exponentiell

Erklärung:

• ISMA: International Securities Market Association
• SIA: Securities Industries Association
• Treasury

Literatur

• Kruschwitz, Lutz (2007); Investitionsrechnung; Oldenbourg; ISBN 978-3-486-58306-9
• Perridon, Louis; Steiner, Manfred: Finanzwirtschaft der Unternehmung, Vahlen, 14. Aufl., 2007, ISBN 3-800-63359-0
• Brealey, Richard A.; Myers, Stewart C. (2003); Principles of Corporate Finance. McGraw-Hill, London, ISBN 0-071-15145-1

Weblinks

• Das Problem mit dem gebundenen Kapital beim internen Zinsfuß