Kirchhoffsches Beugungsintegral

Das Beugungsintegral ermöglicht es, in der Optik die Beugung von Licht durch eine beliebig geformte Blende zu berechnen. Speziell wird dabei, ausgehend von einer einfallenden Elementarwelle und der Blendenfunktion, die die Lichtdurchlässigkeit der Blende beschreibt, die an einem Punkt des Beobachtungsschirms auftreffende Intensität des Lichtes berechnet.

Zwei Grenzfälle des Beugungsintegrals sind die Näherungen für das Fernfeld (Fraunhofer-Beugung) und für das Nahfeld (Fresnel-Beugung). Siehe dazu die entsprechenden Teilabschnitte.

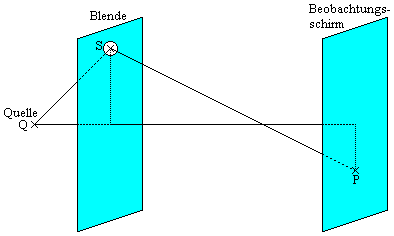
Die obige Skizze zeigt die experimentelle Anordnung, bestehend aus einer Lichtquelle Q, einer Blende S, an der das einfallende Licht gebeugt wird, und einem Beobachtungsschirm, auf dem die auftreffende Lichtintensität an P untersucht wird. Die Form und die Eigenschaften der Blende bestimmen dabei, wie die Intensitätsverteilung auf dem Beobachtungsschirm aussieht.

Hat die Blende z. B. die Form eines Doppelspalts, so ergibt sich als Intensitätsverteilung das bekannte Interferenzmuster. Weitere Anwendungen des Beugungsintegrals sind z. B. Beugungsscheibchen und Klotoide.

Das Kirchhoffsche Beugungsintegral

Das Kirchhoffsche Beugungsintegral, auch Fresnel-Kirchhoffsches Beugungsintegral genannt, lautet

$\psi_P={a_Q\,k_0\over 2\pi\,i}\int_\mathrm{Blende}\mathrm dS\,f_S\,{e^{i\,k_0(d+d_1)}\over d\cdot d_1}\left[{\cos\theta+\cos\tilde{\theta}\over 2}\right].$

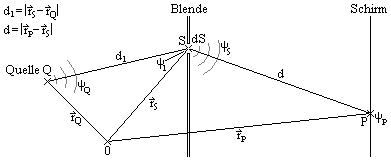
Dabei bezeichnen a_Q die Amplitude der Quelle, k₀ = 2π / λ den Wellenvektor, λ entsprechend die Wellenlänge des Lichtes und schließlich f_S die Blendenfunktion. 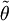$\tilde{\theta}$ und θ sind die Winkel zwischen den mit d₁ bzw. d gekennzeichneten Geraden und einem Lot auf die Blendenebene im Schnittpunkt der Geraden.

Die Intensität am Punkt P auf dem Beobachtungsschirm ergibt sich als Betragsquadrat von ψ_P

$I(P)=| \psi_P |^2={a_Q^2\,k_0^2\over 4\pi^2 }\left|\int_\mathrm{Blende}\mathrm dS\,f_S\,{e^{i\,k_0(d+d_1)}\over d\cdot d_1}\left[{\cos\theta+\cos\tilde{\theta}\over 2}\right]\right|^2.$

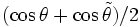Der Term $(\cos\theta+\cos\tilde{\theta})/ 2$ wird Neigungsfaktor genannt und kann in den meisten Anwendungen näherungsweise gleich 1 gesetzt werden.

Fraunhofer- und Fresnel-Beugung

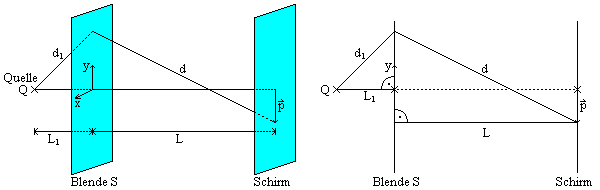
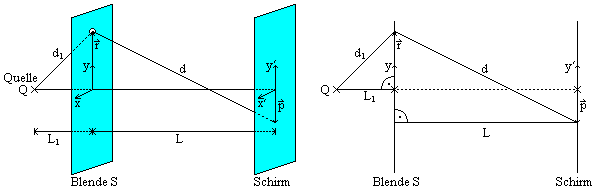
Für die Lichtwege d und d₁ gelten die geometrischen Zusammenhänge (siehe Skizze)

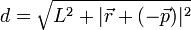$d=\sqrt{L^2+|\vec{r}+(-\vec{p})|^2}$ und

$d_1=\sqrt{L_1^2+r^2}$.

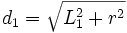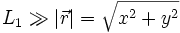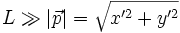Unter den Annahmen $L_1\gg|\vec{r}|=\sqrt{x^2+y^2}$ und $L\gg|\vec{p}|=\sqrt{x'^2+y'^2}$ können die Wurzeln durch eine Taylor-Entwicklung angenähert werden.

Diese Näherung entspricht gerade dem Fall, dass 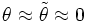$\theta\approx\tilde{\theta}\approx 0$, d. h. für diese Betrachtungen kann der Neigungsfaktor näherungsweise gleich 1 gesetzt werden. Damit lautet das Beugungsintegral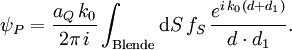

$\psi_P={a_Q\,k_0\over 2\pi\,i}\int_\mathrm{Blende}\mathrm dS\,f_S\,{e^{i\,k_0(d+d_1)}\over d\cdot d_1}.$

Ferner kann wegen der Näherung im Nenner 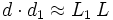$d\cdot d_1\approx L_1\,L$ gesetzt werden. Der Exponent enthält die für die Interferenz wesentliche Phaseninformation und darf nicht auf diese Weise vereinfacht werden. Daraus folgt

$\psi_P={a_Q\,k_0\over 2\pi\,i}{1\over L_1\,L} \int_\mathrm{Blende}\mathrm dS\,f_S\,e^{i\,k_0(d+d_1)}.$

Die Näherung für die Ausdrücke d und d₁, explizit ausgeführt bis zur 2. Ordnung, ergibt

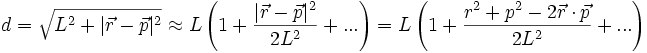$d=\sqrt{L^2+|\vec{r}-\vec{p}|^2}\approx L\left( 1+{|\vec{r}-\vec{p}|^2\over 2L^2}+... \right)= L\left( 1+{r^2+p^2-2\vec{r}\cdot\vec{p}\over 2L^2}+... \right)$ sowie

$d_1=\sqrt{L_1^2+r^2}\approx L_1\left( 1+{r^2\over 2 L_1^2}+... \right).$

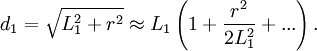
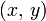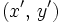Ausgedrückt durch die Koordinaten $(x,\,y)$ und $(x',\,y')$ ergibt das

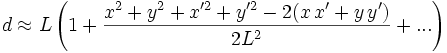$d\approx L\left( 1+{x^2+y^2+x'^2+y'^2-2(x\,x'+y\,y')\over 2L^2}+... \right)$ und

$d_1\approx L_1\left( 1+{x^2+y^2\over 2 L_1^2}+... \right).$

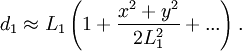
Fraunhofer-Näherung

Die Fraunhofer-Näherung entspricht einer Fernfeld-Näherung, das heißt, dass sowohl die Blendenöffnung als klein als auch die Entfernung des Beobachtungsschirms L als groß angenommen werden. Als Beugungsintegral ergibt sich dabei im Wesentlichen gerade die Fourier-Transformierte der Blendenfunktion. Deshalb spricht man im Rahmen der Fraunhofer-Beugung auch von der Fourier-Optik.

Entsprechend diesen Annahmen werden nur Terme berücksichtigt, die linear in x und y sind, das heißt

$d\approx L\left( 1+{x'^2+y'^2-2(x\,x'+y\,y')\over 2L^2} \right)= L\left( 1+{p^2-2(x\,x'+y\,y')\over 2L^2} \right),$

$d_1\approx L_1.$

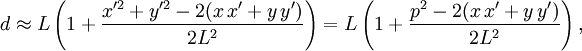
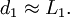
In diesem Fall vereinfacht sich das Beugungsintegral zu

$\psi_P\approx{a_Q\,k_0\over 2\pi\,i}{e^{i\,k_0(L_1+L+{p^2\over 2L})}\over L_1\,L}\int\int_\mathrm{Blende}\mathrm dx\,\mathrm dy\,f_S(x,y)\,e^{-i\,k_0{(x\,x'+y\,y')\over L}}.$

Definiert man einen neuen Wellenvektor 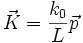$\vec{K}= {k_0\over L}\vec{p}$, so ergibt sich für das Integral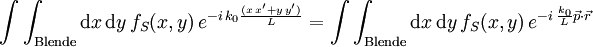

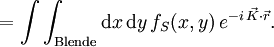
$\int\int_\mathrm{Blende}\mathrm dx\,\mathrm dy\,f_S(x,y)\,e^{-i\,k_0{(x\,x'+y\,y')\over L}} =\int\int_\mathrm{Blende}\mathrm dx\,\mathrm dy\,f_S(x,y)\,e^{-i\,{k_0\over L}\vec{p}\cdot\vec{r}}$ $=\int\int_\mathrm{Blende}\mathrm dx\,\mathrm dy\,f_S(x,y)\,e^{-i\,\vec{K}\cdot\vec{r}}.$

Dies ist gerade die Fourier-Transformierte der Blendenfunktion $f_S\,(x,y)$!

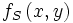Fresnel-Näherung

Die Fresnel-Näherung entspricht einer Nahfeld-Näherung. Hier werden auch quadratische Terme im Exponenten berücksichtigt. Das Beugungsintegral hat dann nicht mehr die einfache Form einer Fourier-Transformierten und ist im Allgemeinen nur numerisch lösbar.

Unter Berücksichtigung quadratischer Terme in x und y ergibt sich

$d\approx L\left( 1+{x^2+y^2+x'^2+y'^2-2(x\,x'+y\,y')\over 2L^2}+... \right),$

$d_1\approx L_1\left( 1+{x^2+y^2\over 2 L_1^2}+... \right).$

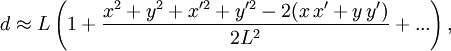
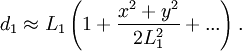
In diesem Fall lautet das Beugungsintegral

$\psi_P={a_Q\,k_0\over 2\pi\,i}{ e^{ i\,k_0(L+L_1+{p^2\over 2L})} \over L\,L_1} \int\int_\mathrm{Blende}\mathrm dx\,\mathrm dy\,f_S(x,y)\,e^{i\,k_0({x^2+y^2-2(x\,x'+y\,y')\over 2L}+{x^2+y^2\over 2 L_1})}.$

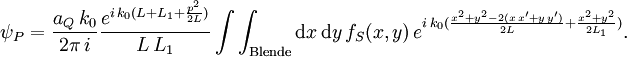
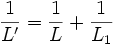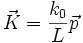Einführung von L' mit ${1\over L'}={1\over L}+{1\over L_1}$ und $\vec{K}= {k_0\over L}\vec{p}$ ergibt dann das Beugungsintegral in Nahfeld-Näherung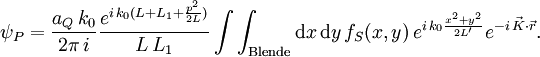

$\psi_P={a_Q\,k_0\over 2\pi\,i}{ e^{ i\,k_0(L+L_1+{p^2\over 2L})} \over L\,L_1} \int\int_\mathrm{Blende}\mathrm dx\,\mathrm dy\,f_S(x,y)\,e^{i\,k_0{x^2+y^2\over 2L'}}e^{-i\,\vec{K}\cdot\vec{r}}.$

Herleitung

Aus der Quelle Q bei 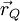$\vec{r}_Q$ tritt die Kugelwelle ψ_Q. a_Q ist die Amplitude der Quelle. Ihre Intensität nimmt linear mit der Entfernung ab (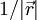$1/|\vec{r}|$). Wellenvektor k mal Abstand 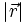$|\vec{r}|$ gibt die Phasenverschiebung der Welle am Ort 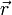$\vec{r}$, Kreisfrequenz ω mal Zeit t die Phasenverschiebung zur Zeit t. Die Welle ist beschrieben durch die Phase am Ort 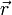$\vec{r}$ zur Zeit t: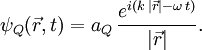

$\psi_Q(\vec{r},t)=a_Q\, {e^{i(k\,|\vec{r}|-\omega\,t)}\over |\vec{r}|}.$

Am Punkt S bei 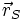$\vec{r}_S$ trifft die Welle im Abstand d₁ auf die Blende. Es sei ψ₁ die Intensität der Welle am Punkt S.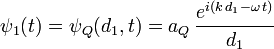

$\psi_1(t)=\psi_Q(d_1,t)=a_Q\,{e^{i(k\,d_1-\omega\,t)}\over d_1}$

Nach dem Huygensschen Prinzip ist der Punkt S Ausgangspunkt einer Elementarwelle, der Sekundärwelle ψ_S.

$\psi_S(\vec{r},t)=a_S\, {e^{i(k\,|\vec{r}|-\omega\,t)}\over |\vec{r}|}.$

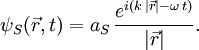
Die Amplitude von ψ_S ist proportional zur Quellen-Amplitude a_Q und zur Blendenfunktion f_S. Die Blendenfunktion gibt die Durchlässigkeit der Blende an. Im einfachsten Fall ist f_S = 1, wenn die Blende geöffnet ist, und f_S = 0, wenn die Blende geschlossen ist. dS ist das infinitesimale Flächenelement der Blendenöffnung am Punkt S.

$a_S(t)\sim f_S\,\mathrm dS\,\psi_1(t)$

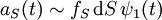
Die Sekundärwelle ψ_S erzeugt im Punkt P bei 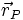$\vec{r}_P$ auf dem Schirm die Wellenintensität dψ_P(t). Sie ist infinitesimal, da nur der Beitrag von dS und nicht aller anderen Punkte auf der Blende betrachtet wird.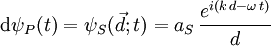

$\mathrm d\psi_P(t)=\psi_S(\vec{d};t)=a_S\,{e^{i(k\,d-\omega\,t)} \over d}$

Die Zeitabhängigkeit 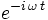$e^{-i\,\omega\,t}$ kann vernachlässigt werden, da sie später beim Rechnen mit Intensitäten ohnehin durch das Betragsquadrat verschwindet.
Durch Einsetzen erhält man: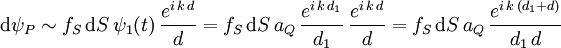

$\mathrm d\psi_P\sim f_S\,\mathrm dS\,\psi_1(t)\,{e^{i\,k\,d} \over d}=f_S\,\mathrm dS\,a_Q\,{e^{i\,k\,d_1} \over d_1}\,{e^{i\,k\,d} \over d}=f_S\,\mathrm dS\,a_Q\,{e^{i\,k\,(d_1+d)} \over d_1\,d}$

Von jedem Punkt auf der Blende geht eine Sekundärwelle aus. Die Intensität ψ_P im Beobachtunspunkt P wird durch die Überlagerung aller Einzelbeiträge erzeugt:

$\psi_P\sim a_Q\int_{Blende}\mathrm dS\,f_S\,{e^{i\,k(d+d_1)}\over d\cdot d_1}.$

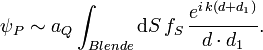
Diese Gleichung erinnert bereits stark an das oben gegebene Beugungsintegral. Mit dem Proportionalitätsfaktor 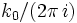$k_0/(2\pi\,i)$ ergibt sich (Neigungswinkel vernachlässigt):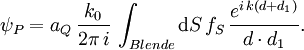

$\psi_P= a_Q\,{k_0 \over 2\pi\,i}\,\int_{Blende}\mathrm dS\,f_S\,{e^{i\,k(d+d_1)}\over d\cdot d_1}.$

Siehe auch

Faltungssatz