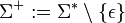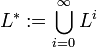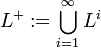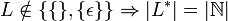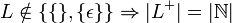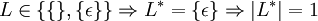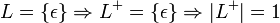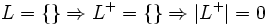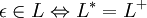Kleenescher Abschluss

Die Kleenesche Hülle (auch endlicher Abschluss, Kleene-*-Abschluss oder Verkettungshülle genannt) eines Alphabets Σ oder einer formalen Sprache L ist die Menge aller Wörter, die durch beliebige Konkatenation (Verknüpfung) von Symbolen des Alphabets Σ bzw. von Wörtern der Sprache L gebildet werden können, wobei das leere Wort ε inbegriffen ist. Sie ist nach dem US-amerikanischen Mathematiker und Logiker Stephen Cole Kleene benannt. Demgegenüber ist die positive Hülle (auch Kleene-+-Abschluss genannt) eines Alphabets Σ oder einer formalen Sprache L die Menge aller Wörter, die aus den Symbolen von Σ beziehungsweise aus Wörtern von L gebildet werden können und die nur dann das leere Wort enthält, wenn die positive Hülle auf eine Sprache angewandt wird, die selbst das leere Wort als Element enthält.

Der Operator der Kleeneschen Hülle ist der Kleene-Stern „. ^* “. So ist die Darstellung der Kleeneschen Hülle eines Alphabets Σ gleich Σ ^* und einer Sprache L gleich L ^* . Demgegenüber ist der Operator der positiven Hülle das Pluszeichen „. ⁺ “, so dass die positive Hülle eines Alphabets Σ mit Σ ⁺ und einer Sprache L mit L ⁺ dargestellt wird.

Definition

Die Kleenesche Hülle eines Alphabets Σ lässt sich strukturell mit Hilfe der strukturellen Induktion definieren. Im Induktionsanfang definiert man zunächst, dass das leere Wort in der Kleeneschen Hülle enthalten ist und im Induktionsschritt wird definiert, dass, wenn das Wort w Element der Kleeneschen Hülle ist, auch die Konkatenationen 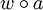$w \circ a$ für alle Symbole 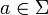$a \in \Sigma$ Elemente der Kleeneschen Hülle sind:

Induktionsanfang: $\epsilon \in \Sigma^*$

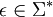
Induktionsschritt: $(w \in \Sigma^*) \and (a \in \Sigma) \Rightarrow w \circ a \in \Sigma^*$

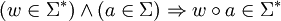
Die positive Hülle eines Alphabets Σ ist definiert als die Kleenesche Hülle dieses Alphabets ohne das leere Wort:

$\Sigma^+ := \Sigma^* \setminus \{ \epsilon \}$

Die Kleenesche Hülle einer Sprache L ist die Vereinigung all ihrer Potenzsprachen:

$L^* := \bigcup_{i=0}^{\infty} L^i$

Die positive Hülle einer Sprache L ist ähnlich definiert, sie ist die Vereinigung aller Potenzen von L größer gleich 1:

$L^+ := \bigcup_{i=1}^{\infty} L^i$

Beispiele

Die Kleenesche Hülle der Sprache L = {aa,bb} ist die Menge aller Wörter, die sich aus aa und bb zusammensetzen, sowie dem leeren Wort:

L ^* = {ε,aa,bb,aaaa,aabb,bbbb,bbaa,bbaabb,aabbaa,...}

Die positive Hülle ist entsprechend:

L ⁺ = {aa,bb,aaaa,aabb,bbbb,bbaa,bbaabb,aabbaa,...}

Die Kleenesche Hülle der leeren Sprache und der Sprache des leeren Wortes enthält nur das leere Wort:

{} ^* = {ε} ^* = {ε}

Die positive Hülle der leeren Sprache ist leer, die der Sprache des leeren Wortes enthält nur das leere Wort:

{} ⁺ = {}

{ε} ⁺ = {ε}

Merkmale

• Die Kleenesche Hülle und die positive Hülle sind jeweils die Trägermenge des Monoids mit der Konkatenation von Wörtern als Operator und dem leeren Wort ε als neutralem Element. Die Kleenesche Hülle sowie die positive Hülle sind damit abgeschlossen gegen der Konkatenation.

• Die Kleenesche und die positive Hülle sind für alle Sprachen, die mindestens ein nicht-leeres Wort enthalten, abzählbar unendlich:

$L\notin \{\{\}, \{\epsilon\}\} \Rightarrow |L^*| = |\mathbb{N}|$

$L\notin \{\{\}, \{\epsilon\}\} \Rightarrow |L^+| = |\mathbb{N}|$

• Die Kleenesche Hülle und die positive Hülle sind für die leere Sprache {} und der Sprache, die nur das leere Wort enthält endlich:

$L\in \{\{\}, \{\epsilon\}\} \Rightarrow L^* = \{\epsilon\} \Rightarrow |L^*| = 1$

$L = \{ \epsilon\} \Rightarrow L^+ = \{ \epsilon \} \Rightarrow |L^+| = 1$

$L = \{ \} \Rightarrow L^+ = \{ \} \Rightarrow |L^+| = 0$

• Wenn eine Sprache L das leere Wort enthält, sind die Kleenesche und die positive Hülle beider Sprachen identisch und umgekehrt:

$\epsilon \in L \Leftrightarrow L^* = L^+$

Literatur

• John E. Hopcroft und Jeffry D. Ullman: Einführung in die Automatentheorie, formale Sprachen und Komplexitätstheorie. Addison Wesley, Bonn 1994, ISBN 3-89319-744-3
• Katrin Erk, Lutz Priese: Theoretische Informatik: eine umfassende Einführung. 2., erw. Auflage. Springer-Verlag, 2002, ISBN 3-540-42624-8, S. 27-29.