Doppelspaltexperiment

Dieser Artikel wurde den Mitarbeitern der Redaktion Physik zur Qualitätssicherung aufgetragen. Wenn Du Dich mit dem Thema auskennst, bist Du herzlich eingeladen, Dich an der Prüfung und möglichen Verbesserung des Artikels zu beteiligen. Der Meinungsaustausch darüber findet derzeit nicht auf der Artikeldiskussionsseite, sondern auf der Qualitätssicherungs-Seite der Physik statt.

Doppelspaltexperiment mit angedeuteten Teilchen

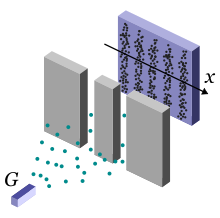
Beim Doppelspaltexperiment lässt man kohärentes Licht (z. B. das eines Lasers) durch eine Blende mit zwei schmalen, parallelen Spalten treten. Dabei ist Voraussetzung, dass die Wellenlänge λ des Lichts kleiner ist als der Abstand a beider Spalte. Auf einem Beobachtungsschirm in einer Distanz zur Blende, die sehr viel größer ist als der Abstand a der Spalte, zeigt sich ein sogenanntes Interferenzmuster. Dieses Muster entsteht durch Beugung des Lichtes an einem Spalt. Bei monochromatischem Licht besteht dieses Muster auf dem Schirm aus hellen Streifen (Maxima) und dunklen Streifen (Minima), ansonsten kommen Farberscheinungen hinzu.

Das Experiment kann nicht nur mit den „Wellen“ des Lichts, sondern auch mit „Teilchen“ (Elektronen, Neutronen, Atomen, Fulleren-Molekülen usw.) durchgeführt werden. Es zeigt sich auch in diesen Fällen ein Interferenzmuster wie bei der Durchführung mit Licht. Das bedeutet, dass auch klassische Teilchen unter bestimmten Bedingungen Welleneigenschaften zeigen – man spricht dann von „Materiewellen“. Mit dem Doppelspaltexperiment kann man so den Welle-Teilchen-Dualismus demonstrieren, der nur im Rahmen der Quantenmechanik erklärt werden kann. Dieses Experiment gilt als das wichtigste Experiment der Quantenmechanik, es ist ein herausragendes Beispiel dafür, wie die Quantenmechanik unsere Weltanschauung verändert.

Geschichte

Thomas Young

1802 führte Thomas Young das Experiment erstmalig durch, um die Wellennatur des Lichtes zu beweisen.

1927 zeigten Clinton Davisson und Lester Germer die Welleneigenschaften von Elektronen anhand der Beugung eines Elektronenstrahls an einem Nickel-Kristall^[1]. Der Kristall wirkt dabei als Reflexionsgitter. Statt zweier Spalte sind hier sehr viele Streuzentren im Spiel.

1961 wurde das Doppelspaltexperiment mit Elektronen durch Claus Jönsson^[2][3] durchgeführt und im September 2002 in einer Umfrage der englischen physikalischen Gesellschaft in der Zeitschrift „Physics World“^[4] zum schönsten physikalischen Experiment aller Zeiten gewählt.

Seither wird das Experiment mit unterschiedlichen Teilchen ständig wiederholt.

Experimentelle Beobachtung

Ergebnis eines Doppelspaltexperiments, welches das Interferenzmuster von Elektronen zeigt. Anzahl Elektronen: 11 (a), 200 (b), 6000 (c), 40000 (d), 140000 (e).

• Die beiden interferierenden Wellen müssen die gleiche Wellenlänge und eine feste Phasenbeziehung zueinander haben, damit überhaupt Interferenz auftreten kann. Diese Voraussetzung kann im Allgemeinen z. B. mit einem Laser (mit hoher Kohärenzlänge) einfach erzielt werden. Welche Folgen eine geringere Kohärenzlänge und variable Phasenbeziehung haben, wird im Artikel Kohärenzlänge genauer diskutiert.
• Da die Lage der hellen und dunklen Streifen des Interferenzmusters von der Wellenlänge abhängig ist, sollte die einfallende Strahlung möglichst monochromatisch sein. Andernfalls überlagern sich mehrere Interferenzmuster, und es kann vorkommen, dass die hellen Streifen des einen Musters die dunklen Streifen des anderen überdecken. Das Interferenzmuster ist dann nicht mehr zu sehen. Je weniger monochromatisch das benutzte Licht ist, desto schlechter ist das Muster zu sehen.
• Deckt man einen der beiden Blendenspalte ab, beobachtet man nun je nach Breite b des Spaltes entweder ein Beugungsmuster am Einzelspalt (b → Wellenlänge λ) oder aber einen breiten, hellen Streifen hinter dem jeweils geöffneten Spalt mit Interferenzmustern hinter den Kanten des Spaltes (b >> λ).
• Versucht man, durch eine beliebige Apparatur herauszufinden, welchen Weg ein bestimmtes Teilchen genommen hat (durch Spalt 1 oder Spalt 2), verschwindet das Interferenzmuster. Diese Information erhält man auch dadurch, dass man einen der Spalte abdeckt. Dieses Verschwinden wird in der Kopenhagener Deutung der Quantenmechanik durch den sogenannten Kollaps der Wellenfunktion erklärt. Das bedeutet, dass das System bei Interferenz in einer Überlagerung der beiden möglichen Wege ist, während eine Messung des tatsächlichen Weges dazu führt, dass auch nur noch dieser „benutzt“ wird. Dies gilt auch, wenn der Weg des Teilchens erst später festgestellt wird.
• Bezüglich des Interferenzmusters muss beachtet werden, dass die Energie des Lichts nicht reduziert wird. Vielmehr handelt es sich lediglich um eine Umverteilung der Energie (Licht) – Die Energie bleibt also erhalten.
• Das Interferenzmuster hängt nicht von der Anzahl oder Gleichzeitigkeit der beteiligten Photonen ab. Bei einer langsamen Folge von einzelnen Teilchen baut sich das Interferenzmuster langsam auf der Photoplatte auf. Nach dem Detektieren von immer mehr Teilchen sieht man die bekannte Verteilung immer genauer. Das ist das eigentlich überraschende, denn jedes einzelne Teilchen „kennt“ die früher oder später kommenden Teilchen nicht, jeder „Durchflug“ eines Teilchens durch den Doppelspalt ist unabhängig von den anderen. Daher muss auch die Verteilung der Wahrscheinlichkeit des Ankommens an den Positionen auf der Photoplatte bei jedem einzelnen Durchflug entstehen. Das lässt sich als Interferenz der Teilchen mit sich selbst interpretieren^[5].

Mathematische Beschreibung

Schematische Darstellung des Doppelspaltexperiments

Wenn der Beobachtungsschirm relativ weit vom Doppelspalt entfernt ist, ist der Winkel α zum Beobachtungspunkt von beiden Spalten aus derselbe. Man kann dann also mit folgendem Bild arbeiten:

Aus der Zeichnung liest man ab:

$\sin{\alpha'}=\frac{\Delta s}{a}$ und $\tan{\alpha}=\frac{x}{d}$

dabei ist:

• a: Spaltmittenabstand
• d: Abstand des Beobachtungsschirms vom Doppelspalt
• x: Entfernung des Beobachtungspunktes auf dem Schirm vom Mittelpunkt
• Δs: Gangunterschied der Wellen von den beiden Spalten zum Beobachtungspunkt

Für kleine Winkel α (Beobachtungsschirm ist weit weg!) gilt die Kleinwinkelnäherung: $\sin{\alpha'} \approx \tan{\alpha}$ also $\frac{\Delta s}{a} \approx \frac{x}{d}$ bzw. $x \approx \Delta s\cdot\frac{d}{a}$

Orte der Maxima

Ein Maximum auf dem Schirm findet man gerade dann, wenn der Gangunterschied Δs der beiden Wellen ein ganzzahliges Vielfaches einer ganzen Wellenlänge λ ist (anders formuliert, analog zu den Minima, ein geradzahliges Vielfaches der halben Wellenlänge). Also $\Delta s=n\cdot\lambda$, wobei $n \in \mathbb{N}_{0}$. Für die Orte der Maxima findet man also:

$x_{\mathrm{max},n}=n\cdot\lambda\cdot\frac{d}{a}$

Orte der Minima

Hier ist der Gangunterschied ein ungerades Vielfaches der halben Wellenlänge. Also $\Delta s=\frac{\lambda}{2}, 3\cdot\frac{\lambda}{2}, 5\cdot\frac{\lambda}{2}, \ldots , (2n-1)\cdot\frac{\lambda}{2}$, wobei $n \in \mathbb{N}$. Für die Orte der Minima ergibt sich also:

$x_{\mathrm{min},n}=(2n-1)\cdot\frac{\lambda}{2}\cdot\frac{d}{a}$

Das Interferenzmuster

Intensitätsmuster hinter einem Doppelspalt (rot). Zum Vergleich ist auch das Beugungsmuster eines entsprechenden Einzelspaltes gezeigt. (blau).

Intensitätsmuster hinter einem Doppelspalt zusammen mit experimentell gemessenen Daten.

Die Intensität des Doppelspaltes lässt sich als Produkt der Intensität des Einzelspaltes und des Gitters mit n = 2 darstellen:

$I(\alpha)=I_0\left(\frac{\sin\gamma}{\gamma}\right)^2\cos^2\delta$

Mit: $\gamma=\frac{k}{2}b\sin\alpha$ und $\delta=\frac{k}{2}a\sin\alpha$

Dabei ist α der Beobachtungswinkel, b die Spaltbreite, a der Spaltabstand und k = 2π/λ die Wellenzahl.

Einfluss von Spaltgeometrie und Wellenlänge

Setzt man für in die Gleichung des Interferenzmusters γ und δ ein, so werden die Einflüsse von Spaltgeometrie und Wellenlänge des einfallenden Lichtes auf das Aussehen des Interferenzmusters deutlich:

$I(\alpha) = I_0 \cdot \left( \frac{\sin\left(\frac{k}{2} b \sin\alpha\right)}{\frac{k}{2} b \sin\alpha} \right)^{\!2} \cdot \cos^2\left(\frac{k}{2} a \sin\alpha\right)$

mit k = 2π/λ.

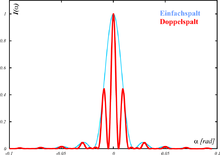
• Eine Änderung der Spaltbreite b führt zu einer Änderung der Lage der Extrema des Einfachspaltes, dessen Intensitätsverteilung (im Bild blau) die Hüllkurve der Intensitätsverteilung des Doppelspalts bildet (im Bild rot)

→ Je breiter der Spalt, desto enger wird die Hüllkurve

• Eine Änderung des Spaltabstandes a führt zu einer Änderung der Lage der Extrema des Doppelspalts innerhalb der konstant bleibenden Hüllkurve

→ Je größer der Spaltabstand, desto enger liegen die Extrema des Doppelspalts beieinander

• Eine Änderung der Wellenlänge λ wirkt sich sowohl auf die Hüllkurve, wie auch auf die Intensitätsverteilung des Doppelspalts aus

→ Je größer die Wellenlänge, desto breiter werden Hüllkurve und die Interferenzabstände des Doppelspalts

Ein gutes Gefühl für den Einfluss der unterschiedlichen Variablen vermittelt das in den Weblinks aufgeführte Java-Applet der Universität Keimyung.

Folgerungen aus den Beobachtungen für die Quantenmechanik

Betrachtet man die quantenmechanische Beschreibung des Experimentes, so fällt eine wichtige Tatsache auf: Der Beobachter muss in die Experimente mit einbezogen werden, da er durch die Detektion bzw. Messung des genauen Weges eines bestimmten Teilchens den Ausgang des Experimentes entscheidend verändert (überraschenderweise kann diese Veränderung aber auch komplett rückgängig gemacht werden, etwa durch einen Quantenradierer). In der klassischen Physik beeinflusst eine Messung nie das Ergebnis eines Versuches.

In der Quantenphysik gibt es mehrere Ansätze, dieses Phänomen zu beschreiben. Alle diese Ansätze (Interpretationen oder Deutungen genannt) führen zum selben Ergebnis, sind aber konzeptuell unterschiedlich. Zwei Deutungen haben sich besonders profiliert:

Kopenhagener Deutung

Der oben erwähnte Kollaps der Wellenfunktion ist diejenige Variante, die heute wohl am weitesten verbreitet ist. Beim Kollaps der Wellenfunktion sagt man, dass das Teilchen alle möglichen Wege gleichzeitig benutzt (linker oder rechter Spalt) und sich nicht „entscheidet“ (es befindet sich in einer sog. Superposition aller möglichen Wege). Mehrere dieser Wege können nun miteinander interferieren und bilden so das erwartete Interferenzmuster. Der Detektor misst dabei aber immer nur ein Teilchen und legt somit seine Position erst fest. Die Wahrscheinlichkeit, das Teilchen an einem bestimmten Ort zu detektieren, ist dabei durch das Interferenzmuster gegeben, das bei der Detektion vieler Teilchen sichtbar wird. Man könnte ein solches Teilchen also als ein „Geisterteilchen“ bezeichnen, auch wenn man keine Möglichkeit hat, dies nachzuweisen, da diese Messung ja den „Geistercharakter“ zerstören würde. Findet nun die Detektion schon vor dem Spalt statt, so stehen nicht mehr alle Wege für die Interferenz zur Verfügung, und es ergibt sich eine andere Verteilung auf dem Schirm (das Interferenzmuster verschwindet). siehe auch Welle-Teilchen-Dualismus

Viele-Welten-Interpretation

Eine weitere Interpretation ist die sog. Viele-Welten-Interpretation. Dort geht man davon aus, dass sich unsere Welt zu jedem Zeitpunkt in unendlich viele parallele Welten aufspaltet, in denen jeweils ein bestimmter Ausgang des Experimentes realisiert ist (z.B. jeweils eine Welt für die Wege 1 und 2). Dies löst das Problem des Geistercharakters der Teilchen, da nun in jeder Welt die Position deterministisch bestimmt ist.

Einzelnachweise

1. ↑ C. Davisson, L. H. Germer: Diffraction of Electrons by a Crystal of Nickel. In: Physical Review. 30, Nr. 6, 1927, S. 705–740, doi:10.1103/PhysRev.30.705.
2. ↑ Claus Jönsson: Elektroneninterferenzen an mehreren künstlich hergestellten Feinspalten. In: Zeitschrift für Physik A Hadrons and Nuclei. 161, Nr. 4, 1961, S. 454-474, doi:10.1007/BF01342460.
3. ↑ C. Jönsson: Electron Diffraction at Multiple Slits. In: American Journal of Physics. 42, 1974, S. 4–11.
4. ↑ Internetpräsenz /Heftarchiv der Zeitschrift Physics World
5. ↑ Was ist Licht?: von der klassischen Optik zur Quantenoptik, Thomas Walther und Herbert Walther, CH Beck, 2004, Seite 91 ff.

Literatur

• John Gribbin: Auf der Suche nach Schrödingers Katze. Quantenphysik und Wirklichkeit.. 5. Auflage. Piper, 2004, ISBN 3492240305.
• Claus Jönsson: Interferenz von Elektronen am Doppelspalt. In: Zeitschrift für Physik, Nr. 161, 1961, Seiten 454–474
• David Halliday, Robert Resnick, Jearl Walker: Physik. 2. Auflage. Wiley-VCH, 2003, ISBN 3527403663.
• Wolfgang Demtröder: Experimentalphysik. Bd.2 : Elektrizität und Optik. 3.. Auflage. Springer, Berlin, 2004, ISBN 3540202102.

Weblinks

 Commons: Doppelspaltexperiment – Sammlung von Bildern, Videos und Audiodateien

 Wiktionary: Doppelspaltexperiment – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Doppelspaltversuch – Einführung mit interaktiven Animationen (Universität Ulm)
• Spaltversuche mit Licht – Java-Applet der Universität Keimyung (Korea) auf LEIFI-Physik
• Doppelspaltversuch mit nicht-monochromatischem und monochromatischen Licht im Vergleich (Uni Hannover)