Konchoide von Dürer

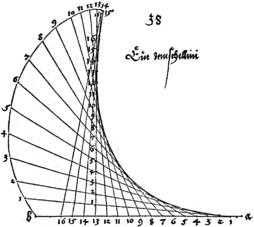
Die Konchoide von Dürer, oder auch Muschellinie, ist eine spezielle ebene algebraische Kurve. Albrecht Dürer zeichnete sie erstmals in seinem Buch Underweysung der Messung (S. 38) und nannte sie „ein muschellini”.

Dürers Konstruktion der Muschellinie

Gleichung

• Kartesische Koordinaten: (y² + xy + ay − b²)² = (b² − y²)(y − x + a)²

• Parametergleichung (2 Kurvenäste):

$x(t) = t + \frac{b(a-t)}{\sqrt{a^2-2at + 2t^2}}\; ,\ y(t) = \frac{bt}{\sqrt{a^2-2at + 2t^2}},$

$x(t) = t - \frac{b(a+t)}{\sqrt{a^2-2at + 2t^2}}\; ,\ y(t) = -\frac{bt}{\sqrt{a^2-2at + 2t^2}}.$

(Der zweite Kurvenast wurde von Dürer nicht entdeckt.)

Eigenschaften

• Für a = 0 entartet die Kurve zu dem Geradenpaar $y=\pm b / \sqrt2$ und einem Kreis x² + y² = b².

• Für b = 0 entarten die beiden Kurvenäste zu der Geraden y = 0.

• Für b = 2a hat die Kurve eine Spitze bei (x,y) = ( − 2a,a).

Siehe auch

• Konchoide

Weblinks

• Darstellungen und Dürers Konstruktion der Kurve (von I. Rubin; PDF-Datei; 144 kB)
• Information zur Kurve (engl.)