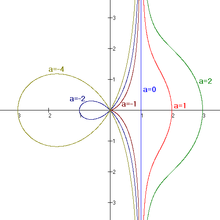
Konchoide von de Sluze

Die Konchoide von de Sluze für verschiedene Werte von a

Die Konchoide von de Sluze ist eine Schar von ebenen Kurven die 1662 von René François Walther de Sluze untersucht wurde. In Polarkoordinaten wird sie wie folgt ausgedrückt:

r = sec θ + acos θ

Für kartesische Koordinaten (x,y) gilt:

(x − 1)(x² + y²) = ax²

Die kartesische Form hat jedoch für a=0 einen Lösungspunkt (0,0), der in der Polarkoordinatenform nicht vorhanden ist.

Diese Ausdrücke haben eine Asymptote x=1 (für a≠0). Der Punkt, der von der Asymptote a am weitesten entfernt liegt, ist (1+a,0). In (0,0) kreuzen sich Kurven für a<−1 selbst.

Die Fläche zwischen Kurve und der Asymptote berechnet sich wie folgt:

$|a|(1+a/4)\pi\,$ für a≥−1

$\left(1-\frac a2\right)\sqrt{-(a+1)}-a\left(2+\frac a2\right)\arcsin\frac1{\sqrt{-a}}$ für a<−1

Die Fläche der Schleife ist

$\left(2+\frac a2\right)a\arccos\frac1{\sqrt{-a}} + \left(1-\frac a2\right)\sqrt{-(a+1)}$ für a<−1

Vier Kurven der Schar haben spezielle Namen:

• a=0, Gerade (Asymptote für den Rest der Schar)
• a=−1, Zissoide (clue to geometric construction)
• a=−2, rechte Strophoide
• a=−4, Trisektrix von Maclaurin

Weblinks

• Eric W. Weisstein: Conchoid of de Sluze. In: MathWorld. (englisch)
• Conchoid of de Sluze. In: MacTutor History of Mathematics archive (englisch)